Arcsine distribution
|
Probability density function
| |
|
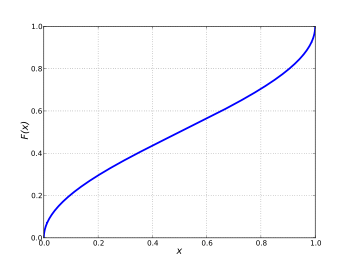
Cumulative distribution function
| |
| Parameters | none |
|---|---|
| Support | |
| CDF | |
| Mean | |
| Median | |
| Mode | |
| Variance | |
| Skewness | |
| Ex. kurtosis | |
| Entropy | |
| MGF | |
| CF | |
In probability theory, the arcsine distribution is the probability distribution whose cumulative distribution function is
for 0 ≤ x ≤ 1, and whose probability density function is
on (0, 1). The standard arcsine distribution is a special case of the beta distribution with α = β = 1/2. That is, if is the standard arcsine distribution then
The arcsine distribution appears
- in the Lévy arcsine law;
- in the Erdős arcsine law;
- as the Jeffreys prior for the probability of success of a Bernoulli trial.
Generalization
| Parameters | |
|---|---|
| Support | |
| CDF | |
| Mean | |
| Median | |
| Mode | |
| Variance | |
| Skewness | |
| Ex. kurtosis |
Arbitrary bounded support
The distribution can be expanded to include any bounded support from a ≤ x ≤ b by a simple transformation
for a ≤ x ≤ b, and whose probability density function is
on (a, b).
Shape factor
The generalized standard arcsine distribution on (0,1) with probability density function
is also a special case of the beta distribution with parameters .
Note that when the general arcsine distribution reduces to the standard distribution listed above.
Properties
- Arcsine distribution is closed under translation and scaling by a positive factor
- If
- The square of an arc sine distribution over (-1, 1) has arc sine distribution over (0, 1)
- If
Related distributions
- If U and V are i.i.d uniform (−π,π) random variables, then , , , and all have an distribution.
- If is the generalized arcsine distribution with shape parameter supported on the finite interval [a,b] then
See also
References
- Rogozin, B.A. (2001), "A/a013160", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4