Systolic geometry
In mathematics, systolic geometry is the study of systolic invariants of manifolds and polyhedra, as initially conceived by Charles Loewner and developed by Mikhail Gromov, Michael Freedman, Peter Sarnak, Mikhail Katz, Larry Guth, and others, in its arithmetical, ergodic, and topological manifestations. See also a slower-paced Introduction to systolic geometry.
The notion of systole

The systole of a compact metric space X is a metric invariant of X, defined to be the least length of a noncontractible loop in X (i.e. a loop that cannot be contracted to a point in the ambient space X). In more technical language, we minimize length over free loops representing nontrivial conjugacy classes in the fundamental group of X. When X is a graph, the invariant is usually referred to as the girth, ever since the 1947 article on girth by W. T. Tutte.[1] Possibly inspired by Tutte's article, Loewner started thinking about systolic questions on surfaces in the late 1940s, resulting in a 1950 thesis by his student Pao Ming Pu. The actual term "systole" itself was not coined until a quarter century later, by Marcel Berger.
This line of research was, apparently, given further impetus by a remark of René Thom, in a conversation with Berger in the library of Strasbourg University during the 1961-62 academic year, shortly after the publication of the papers of R. Accola and C. Blatter. Referring to these systolic inequalities, Thom reportedly exclaimed: Mais c'est fondamental! [These results are of fundamental importance!]
Subsequently, Berger popularized the subject in a series of articles and books, most recently in the March 2008 issue of the Notices of the American Mathematical Society (see reference below). A bibliography at the Website for systolic geometry and topology currently contains over 160 articles. Systolic geometry is a rapidly developing field, featuring a number of recent publications in leading journals. Recently (see the 2006 paper by Katz and Rudyak below), the link with the Lusternik–Schnirelmann category has emerged. The existence of such a link can be thought of as a theorem in systolic topology.
Property of a centrally symmetric polyhedron in 3-space
Every convex centrally symmetric polyhedron P in R3 admits a pair of opposite (antipodal) points and a path of length L joining them and lying on the boundary ∂P of P, satisfying
An alternative formulation is as follows. Any centrally symmetric convex body of surface area A can be squeezed through a noose of length , with the tightest fit achieved by a sphere. This property is equivalent to a special case of Pu's inequality (see below), one of the earliest systolic inequalities.
Concepts
To give a preliminary idea of the flavor of the field, one could make the following observations. The main thrust of Thom's remark to Berger quoted above appears to be the following. Whenever one encounters an inequality relating geometric invariants, such a phenomenon in itself is interesting; all the more so when the inequality is sharp (i.e., optimal). The classical isoperimetric inequality is a good example.

In systolic questions about surfaces, integral-geometric identities play a particularly important role. Roughly speaking, there is an integral identity relating area on the one hand, and an average of energies of a suitable family of loops on the other. By the Cauchy-Schwarz inequality, energy is an upper bound for length squared; hence one obtains an inequality between area and the square of the systole. Such an approach works both for the Loewner inequality
for the torus, where the case of equality is attained by the flat torus whose deck transformations form the lattice of Eisenstein integers,

and for Pu's inequality for the real projective plane P2(R):
- ,
with equality characterizing a metric of constant Gaussian curvature.
An application of the computational formula for the variance in fact yields the following version of Loewner's torus inequality with isosystolic defect:
where f is the conformal factor of the metric with respect to a unit area flat metric in its conformal class. This inequality can be thought of as analogous to Bonnesen's inequality with isoperimetric defect, a strengthening of the isoperimetric inequality.
A number of new inequalities of this type have recently been discovered, including universal volume lower bounds. More details appear at systoles of surfaces.
Gromov's systolic inequality
The deepest result in the field is Gromov's inequality for the homotopy 1-systole of an essential n-manifold M:
where Cn is a universal constant only depending on the dimension of M. Here the homotopy systole sysπ1 is by definition the least length of a noncontractible loop in M. A manifold is called essential if its fundamental class [M] represents a nontrivial class in the homology of its fundamental group. The proof involves a new invariant called the filling radius, introduced by Gromov, defined as follows.
Denote by A the coefficient ring Z or Z2, depending on whether or not M is orientable. Then the fundamental class, denoted [M], of a compact n-dimensional manifold M is a generator of . Given an imbedding of M in Euclidean space E, we set
where ιε is the inclusion homomorphism induced by the inclusion of M in its ε-neighborhood Uε M in E.
To define an absolute filling radius in a situation where M is equipped with a Riemannian metric g, Gromov proceeds as follows. One exploits an imbedding due to C. Kuratowski. One imbeds M in the Banach space L∞(M) of bounded Borel functions on M, equipped with the sup norm . Namely, we map a point x ∈ M to the function fx ∈ L∞(M) defined by the formula fx(y) = d(x,y) for all y ∈ M, where d is the distance function defined by the metric. By the triangle inequality we have and therefore the imbedding is strongly isometric, in the precise sense that internal distance and ambient distance coincide. Such a strongly isometric imbedding is impossible if the ambient space is a Hilbert space, even when M is the Riemannian circle (the distance between opposite points must be π, not 2!). We then set E = L∞(M) in the formula above, and define
Namely, Gromov proved a sharp inequality relating the systole and the filling radius,
valid for all essential manifolds M; as well as an inequality
valid for all closed manifolds M.
A summary of a proof, based on recent results in geometric measure theory by S. Wenger, building upon earlier work by L. Ambrosio and B. Kirchheim, appears in Section 12.2 of the book "Systolic geometry and topology" referenced below. A completely different approach to the proof of Gromov's inequality was recently proposed by Larry Guth.[2]
Gromov's stable inequality
A significant difference between 1-systolic invariants (defined in terms of lengths of loops) and the higher, k-systolic invariants (defined in terms of areas of cycles, etc.) should be kept in mind. While a number of optimal systolic inequalities, involving the 1-systoles, have by now been obtained, just about the only optimal inequality involving purely the higher k-systoles is Gromov's optimal stable 2-systolic inequality
for complex projective space, where the optimal bound is attained by the symmetric Fubini–Study metric, pointing to the link to quantum mechanics. Here the stable 2-systole of a Riemannian manifold M is defined by setting
where is the stable norm, while λ1 is the least norm of a nonzero element of the lattice. Just how exceptional Gromov's stable inequality is, only became clear recently. Namely, it was discovered that, contrary to expectation, the symmetric metric on the quaternionic projective plane is not its systolically optimal metric, in contrast with the 2-systole in the complex case. While the quaternionic projective plane with its symmetric metric has a middle-dimensional stable systolic ratio of 10/3, the analogous ratio for the symmetric metric of the complex projective 4-space gives the value 6, while the best available upper bound for such a ratio of an arbitrary metric on both of these spaces is 14. This upper bound is related to properties of the Lie algebra E7. If there exists an 8-manifold with exceptional Spin(7) holonomy and 4-th Betti number 1, then the value 14 is in fact optimal. Manifolds with Spin(7) holonomy have been studied intensively by Dominic Joyce.
Lower bounds for 2-systoles
Similarly, just about the only nontrivial lower bound for a k-systole with k = 2, results from recent work in gauge theory and J-holomorphic curves. The study of lower bounds for the conformal 2-systole of 4-manifolds has led to a simplified proof of the density of the image of the period map, by Jake Solomon.
Schottky problem
Perhaps one of the most striking applications of systoles is in the context of the Schottky problem, by P. Buser and P. Sarnak, who distinguished the Jacobians of Riemann surfaces among principally polarized abelian varieties, laying the foundation for systolic arithmetic.
Lusternik–Schnirelmann category
Asking systolic questions often stimulates questions in related fields. Thus, a notion of systolic category of a manifold has been defined and investigated, exhibiting a connection to the Lusternik–Schnirelmann category (LS category). Note that the systolic category (as well as the LS category) is, by definition, an integer. The two categories have been shown to coincide for both surfaces and 3-manifolds. Moreover, for orientable 4-manifolds, systolic category is a lower bound for LS category. Once the connection is established, the influence is mutual: known results about LS category stimulate systolic questions, and vice versa.
The new invariant was introduced by Katz and Rudyak (see below). Since the invariant turns out to be closely related to the Lusternik-Schnirelman category (LS category), it was called systolic category.
Systolic category of a manifold M is defined in terms of the various k-systoles of M. Roughly speaking, the idea is as follows. Given a manifold M, one looks for the longest product of systoles which give a "curvature-free" lower bound for the total volume of M (with a constant independent of the metric). It is natural to include systolic invariants of the covers of M in the definition, as well. The number of factors in such a "longest product" is by definition the systolic category of M.
For example, Gromov showed that an essential n-manifold admits a volume lower bound in terms of the n'th power of the homotopy 1-systole (see section above). It follows that the systolic category of an essential n-manifold is precisely n. In fact, for closed n-manifolds, the maximal value of both the LS category and the systolic category is attained simultaneously.
Another hint at the existence of an intriguing relation between the two categories is the relation to the invariant called the cuplength. Thus, the real cuplength turns out to be a lower bound for both categories.
Systolic category coincides with the LS category in a number of cases, including the case of manifolds of dimensions 2 and 3. In dimension 4, it was recently shown that the systolic category is a lower bound for the LS category.
Systolic hyperbolic geometry
The study of the asymptotic behavior for large genus g of the systole of hyperbolic surfaces reveals some interesting constants. Thus, Hurwitz surfaces Σg defined by a tower of principal congruence subgroups of the (2,3,7) hyperbolic triangle group satisfy the bound
and a similar bound holds for more general arithmetic Fuchsian groups. This 2007 result by Katz, Schaps, and Vishne generalizes the results of Peter Sarnak and Peter Buser in the case of arithmetic groups defined over Q, from their seminal 1994 paper (see below).
A bibliography for systoles in hyperbolic geometry currently numbers forty articles. Interesting examples are provided by the Bolza surface, Klein quartic, Macbeath surface, First Hurwitz triplet.
Relation to Abel–Jacobi maps
A family of optimal systolic inequalities is obtained as an application of the techniques of Burago and Ivanov, exploiting suitable Abel–Jacobi maps, defined as follows.
Let M be a manifold, π = π1(M), its fundamental group and f: π → πab be its abelianisation map. Let tor be the torsion subgroup of πab. Let g: πab → πab/tor be the quotient by torsion. Clearly, πab/tor= Zb, where b = b1 (M). Let φ: π → Zb be the composed homomorphism.
Definition: The cover of the manifold M corresponding the subgroup Ker(φ) ⊂ π is called the universal (or maximal) free abelian cover.
Now assume M has a Riemannian metric. Let E be the space of harmonic 1-forms on M, with dual E* canonically identified with H1(M,R). By integrating an integral harmonic 1-form along paths from a basepoint x0 ∈ M, we obtain a map to the circle R/Z = S1.
Similarly, in order to define a map M → H1(M,R)/H1(M,Z)R without choosing a basis for cohomology, we argue as follows. Let x be a point in the universal cover of M. Thus x is represented by a point of M together with a path c from x0 to it. By integrating along the path c, we obtain a linear form, , on E. We thus obtain a map , which, furthermore, descends to a map
where is the universal free abelian cover.
Definition: The Jacobi variety (Jacobi torus) of M is the torus J1(M)= H1(M,R)/H1(M,Z)R
Definition: The Abel–Jacobi map is obtained from the map above by passing to quotients. The Abel–Jacobi map is unique up to translations of the Jacobi torus.
As an example one can cite the following inequality, due to D. Burago, S. Ivanov and M. Gromov.
Let M be an n-dimensional Riemannian manifold with first Betti number n, such that the map from M to its Jacobi torus has nonzero degree. Then M satisfies the optimal stable systolic inequality
where is the classical Hermite constant.
Related fields, volume entropy
Asymptotic phenomena for the systole of surfaces of large genus have been shown to be related to interesting ergodic phenomena, and to properties of congruence subgroups of arithmetic groups.
Gromov's 1983 inequality for the homotopy systole implies, in particular, a uniform lower bound for the area of an aspherical surface in terms of its systole. Such a bound generalizes the inequalities of Loewner and Pu, albeit in a non-optimal fashion.
Gromov's seminal 1983 paper also contains asymptotic bounds relating the systole and the area, which improve the uniform bound (valid in all dimensions).
It was discovered recently (see paper by Katz and Sabourau below) that the volume entropy h, together with A. Katok's optimal inequality for h, is the "right" intermediary in a transparent proof of M. Gromov's asymptotic bound for the systolic ratio of surfaces of large genus.
The classical result of A. Katok states that every metric on a closed surface M with negative Euler characteristic satisfies an optimal inequality relating the entropy and the area.
It turns out that the minimal entropy of a closed surface can be related to its optimal systolic ratio. Namely, there is an upper bound for the entropy of a systolically extremal surface, in terms of its systole. By combining this upper bound with Katok's optimal lower bound in terms of the volume, one obtains a simpler alternative proof of Gromov's asymptotic estimate for the optimal systolic ratio of surfaces of large genus. Furthermore, such an approach yields an improved multiplicative constant in Gromov's theorem.
As an application, this method implies that every metric on a surface of genus at least 20 satisfies Loewner's torus inequality. This improves the best earlier estimate of 50 which followed from an estimate of Gromov's.
Filling area conjecture
Gromov's filling area conjecture has been proved in a hyperelliptic setting (see reference by Bangert et al. below).
The filling area conjecture asserts that among all possible fillings of the Riemannian circle of length 2π by a surface with the strongly isometric property, the round hemisphere has the least area. Here the Riemannian circle refers to the unique closed 1-dimensional Riemannian manifold of total 1-volume 2π and Riemannian diameter π.
To explain the conjecture, we start with the observation that the equatorial circle of the unit 2-sphere, S2 ⊂ R3, is a Riemannian circle S1 of length 2π and diameter π.
More precisely, the Riemannian distance function of S1 is the restriction of the ambient Riemannian distance on the sphere. This property is not satisfied by the standard imbedding of the unit circle in the Euclidean plane, where a pair of opposite points are at distance 2, not π.
We consider all fillings of S1 by a surface, such that the restricted metric defined by the inclusion of the circle as the boundary of the surface is the Riemannian metric of a circle of length 2π. The inclusion of the circle as the boundary is then called a strongly isometric imbedding of the circle.
In 1983 Gromov conjectured that the round hemisphere gives the "best" way of filling the circle among all filling surfaces.
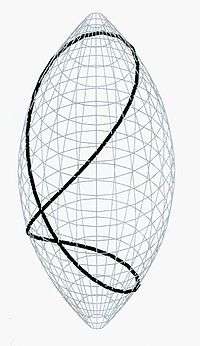
The case of simply-connected fillings is equivalent to Pu's inequality. Recently the case of genus-1 fillings was settled affirmatively, as well (see reference by Bangert et al. below). Namely, it turns out that one can exploit a half-century old formula by J. Hersch from integral geometry. Namely, consider the family of figure-8 loops on a football, with the self-intersection point at the equator (see figure at the beginning of the article). Hersch's formula expresses the area of a metric in the conformal class of the football, as an average of the energies of the figure-8 loops from the family. An application of Hersch's formula to the hyperelliptic quotient of the Riemann surface proves the filling area conjecture in this case.
Other systolic ramifications of hyperellipticity have been identified in genus 2.
Surveys
The surveys in the field include M. Berger's survey (1993), Gromov's survey (1996), Gromov's book (1999), Berger's panoramic book (2003), as well as Katz's book (2007). These references may help a beginner enter the field. They also contain open problems to work on.
See also
- systoles of surfaces
- Loewner's torus inequality
- Pu's inequality
- Filling area conjecture
- Gromov's inequality for complex projective space
- Gromov's systolic inequality for essential manifolds
- First Hurwitz triplet
- List of differential geometry topics
- Systolic freedom
- Girth (functional analysis)
Notes
- ↑ Tutte, William T. (1947). "A family of cubical graphs". Proc. Cambridge Philos. Soc. 43 (4): 459–474. doi:10.1017/S0305004100023720. MR 0021678.
- ↑ Guth, Larry (2011). "Volumes of balls in large Riemannian manifolds". Annals of Mathematics. 173 (1): 51–76. arXiv:math/0610212
 . doi:10.4007/annals.2011.173.1.2. MR 2753599.
. doi:10.4007/annals.2011.173.1.2. MR 2753599.
References
- Bangert, V.; Croke, C.; Ivanov, S.; Katz, M.: Filling area conjecture and ovalless real hyperelliptic surfaces. Geometric and Functional Analysis (GAFA) 15 (2005), no. 3, 577–597.
- Berger, M.: Systoles et applications selon Gromov. (French. French summary) [Systoles and their applications according to Gromov] Séminaire Bourbaki, Vol. 1992/93. Astérisque No. 216 (1993), Exp. No. 771, 5, 279—310.
- Berger, M.: A panoramic view of Riemannian geometry. Springer-Verlag, Berlin, 2003.
- Berger, M.: What is... a Systole? Notices of the AMS 55 (2008), no. 3, 374–376.
- Buser, P.; Sarnak, P.: On the period matrix of a Riemann surface of large genus. With an appendix by J. H. Conway and N. J. A. Sloane. Invent. Math. 117 (1994), no. 1, 27—56.
- Gromov, M.: Filling Riemannian manifolds, J. Diff. Geom. 18 (1983), 1–147.
- Gromov, M. Systoles and intersystolic inequalities. (English, French summary) Actes de la Table Ronde de Géométrie Différentielle (Luminy, 1992), 291—362, Sémin. Congr., 1, Soc. Math. France, Paris, 1996.
- Gromov, M. Metric Structures for Riemannian and Non-Riemannian Spaces. Based on the 1981 French original. With appendices by Mikhail Katz, Pierre Pansu, and Stephen Semmes. Translated from the French by Sean Michael Bates. Progress in Mathematics, 152. Birkhäuser Boston, Inc., Boston, Massachusetts, 1999.
- Katz, M.: The filling radius of two-point homogeneous spaces. Journal of Differential Geometry 18, Number 3 (1983), 505-511.
- Katz, M. Systolic geometry and topology. With an appendix by J. Solomon. Mathematical Surveys and Monographs, volume 137. American Mathematical Society, 2007.
- Katz, M.; Rudyak, Y.: Systolic category and Lusternik–Schnirelman category of low-dimensional manifolds. Communications on Pure and Applied Mathematics 59 ('06), 1433–1456.
- Katz, M.; Sabourau, S.: Entropy of systolically extremal surfaces and asymptotic bounds. Ergo. Th. Dynam. Sys. 25 (2005), 1209–1220.
- Katz, M.; Schaps, M.; Vishne, U.: Logarithmic growth of systole of arithmetic Riemann surfaces along congruence subgroups. J. Differential Geom. 76 (2007), no. 3, 399–422. Available at arXiv:math.DG/0505007
- Pu, P. M.: Some inequalities in certain nonorientable Riemannian manifolds. Pacific J. Math. 2 (1952), 55—71.