Scale-step
In Schenkerian theory, a scale-step (German: Stufe) is a triad (based on one of the diatonic scale degrees) that is perceived as an organizing force for a passage of music (in accordance with the principle of composing-out). In Harmony, Schenker gives the following example and asserts that
- our ear will connect the first tone, G, with the B on the first quarter of measure 1 as the third of G.
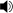 Play
Play - Likewise, it will connect that G with the D on the first quarter of measure 2 as its fifth. Our ear will establish this connection instinctively, but nonetheless in accordance with the demands of Nature. In an analogous way, it will link that first G with the C and E of the second half of measure 1 and thus form the concept of another triad. For our ear will miss no opportunity to hear such triads, no matter how far in the background of our consciousness this conception may lie hidden and no matter whether in the plan of the composition it is overshadowed by far more obvious and important relationships."[1]
A scale-step triad is designated by an uppercase Roman numeral representing the scale degree of the root, much as in traditional "harmonic analysis" (see chord progression). Thus, in the above example (which is in G major), the G major triad that Schenker claims we perceive through the first two measures would be labelled "I". However, unlike traditional harmonic analyses, Schenker's theory is not concerned with the mere labelling of such chords, but rather with discerning hierarchical relationships among tones. For Schenker, the chords occurring in a passage need not be of equal import. As he explains:
The scale-step is a higher and more abstract unit [than the mere "chord"]. At times it may even comprise several harmonies, each of which could be considered individually as an independent triad or seventh-chord; in other words: even if, under certain circumstances, a certain number of harmonies look like independent triads, or seventh-chords, they may nonetheless add up, in their totality, to one single triad, e.g. C-E-G, and they would have to be subsumed under the concept of this triad on C as a scale-step. The scale-step asserts its higher or more general character by comprising or summarizing the individual phenomena and embodying their intrinsic unity in one single triad.[2]
Furthermore, in terms of Schenker's mature theory, the question of whether a given triad possesses scale-step status depends on the structural level under discussion. Indeed, it follows from Schenker's concepts that, at the highest level, a tonal composition possesses only one scale step, since the entirety of the work may be understood as an elaboration of its tonic triad (i.e. scale-step I).
Notes
- ↑ Schenker 1954: 133-134, section §76.
- ↑ Schenker 1954: 139
References
- Schenker, Heinrich; ed. and annot. Oswald Jonas (1954). Harmony. trans. Elisabeth Mann-Borgese. Chicago: University of Chicago Press. OCLC 280916. Cite uses deprecated parameter
|coauthors=(help)
