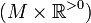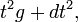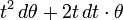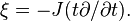Sasakian manifold
In differential geometry, a Sasakian manifold (named after Shigeo Sasaki) is a contact manifold  equipped with a special kind of Riemannian metric
equipped with a special kind of Riemannian metric  , called a Sasakian metric.
, called a Sasakian metric.
Definition
A Sasakian metric is defined using the construction of the Riemannian cone. Given a Riemannian manifold 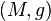 , its Riemannian cone is a product
, its Riemannian cone is a product
of 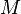 with a half-line
with a half-line 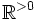 ,
equipped with the cone metric
,
equipped with the cone metric
where  is the parameter in
is the parameter in 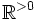 .
.
A manifold 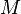 equipped with a 1-form
equipped with a 1-form  is contact if and only if the 2-form
is contact if and only if the 2-form
on its cone is symplectic (this is one of the possible definitions of a contact structure). A contact Riemannian manifold is Sasakian, if its Riemannian cone with the cone metric is a Kähler manifold with Kähler form
Examples
As an example consider
where the right hand side is a natural Kähler manifold and read as the cone over the sphere (endowed with embedded metric). The contact 1-form on  is the form associated to the tangent vector
is the form associated to the tangent vector  , constructed from the unit-normal vector
, constructed from the unit-normal vector 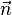 to the sphere (
to the sphere (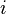 being the complex structure on
being the complex structure on  ).
).
Another non-compact example is 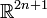 with coordinates
with coordinates  endowed with contact-form
endowed with contact-form
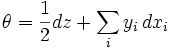
and the Riemannian metric

As a third example consider:

where the right hand side has a natural Kähler structure (and the  acts by reflection at the origin).
acts by reflection at the origin).
History
Sasakian manifolds were introduced in 1960 by the Japanese geometer Shigeo Sasaki.[1] There was not much activity in this field after the mid-1970s, until the advent of String theory. Since then Sasakian manifolds have gained prominence in physics and algebraic geometry, mostly due to a string of papers by Boyer, Galicki and their co-authors.
The Reeb vector field
The homothetic vector field on the cone over a Sasakian manifold is defined to be
As the cone is by definition Kähler, there exists a complex structure J. The Reeb vector field on the Sasaskian manifold is defined to be
It is nowhere vanishing. It commutes with all holomorphic Killing vectors on the cone and in particular with all isometries of the Sasakian manifold. If the orbits of the vector field close then the space of orbits is a Kähler orbifold. The Reeb vector field at the Sasakian manifold at unit radius is a unit vector field and tangential to the embedding.
Sasaki–Einstein manifolds
A Sasakian manifold 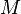 is one with the Riemannian cone Kähler.
If the cone is, in addition, Ricci-flat,
is one with the Riemannian cone Kähler.
If the cone is, in addition, Ricci-flat, 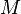 is called Sasaki–Einstein; if it is hyperkähler,
is called Sasaki–Einstein; if it is hyperkähler, 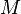 is called 3-Sasakian. Any 3-Sasakian manifold is an Einstein manifold and a spin manifold.
is called 3-Sasakian. Any 3-Sasakian manifold is an Einstein manifold and a spin manifold.
Examples include all round odd-dimensional spheres, and the product of a 2-sphere and a 3-sphere with a homogeneous metric. The cones are respectively complex vector spaces without the origin, and the conifold.
It is also known that there exist Sasaki-Einstein metrics on some circle bundles over the 3rd through 8th del Pezzo surfaces.
In 2005 an infinite family of 5-dimensional Sasaki-Einstein metrics was constructed. These are denoted
where a, b and c are three integral parameters. A 2-parameter family had been constructed the previous year, before which only a finite number of 5-dimensional examples were known.
Notes
References
- S. Sasaki, "On differentiable manifolds with certain structures which are closely related to almost contact structure", Tohoku Math. J. 2 (1960), 459-476.
- Charles P. Boyer, Krzysztof Galicki, Sasakian geometry
- Charles P. Boyer, Krzysztof Galicki, "3-Sasakian Manifolds", Surveys Diff. Geom. 7 (1999) 123-184
- Dario Martelli, James Sparks and Shing-Tung Yau, "Sasaki-Einstein Manifolds and Volume Minimization", ArXiv hep-th/0603021