Prime avoidance lemma
In algebra, the prime avoidance lemma says that if an ideal I in a commutative ring R is contained in a union of finitely many prime ideals Pi's, then it is contained in Pi for some i.
There are many variations of the lemma (cf. Hochster); for example, if the ring R contains an infinite field or a finite field of sufficiently large cardinality, then the statement follows from a fact in linear algebra that a vector space over an infinite field or a finite field of large cardinality is not a finite union of its proper vector subspaces.[1]
Statement and proof
The following statement and argument are perhaps the most standard.
Statement: Let E be a subset of R that is an additive subgroup of R and is multiplicatively closed. Let  be ideals such that
be ideals such that  are prime ideals for
are prime ideals for  . If E is not contained in any of
. If E is not contained in any of  's, then E is not contained in the union
's, then E is not contained in the union  .
.
Proof by induction on n: The idea is to find an element that is in E and not in any of  's. The basic case n = 1 is trivial. Next suppose n ≥ 2. For each i choose
's. The basic case n = 1 is trivial. Next suppose n ≥ 2. For each i choose
where the set on the right is nonempty by inductive hypothesis. We can assume  for all i; otherwise, some
for all i; otherwise, some  avoids all the
avoids all the  's and we are done. Put
's and we are done. Put
 .
.
Then z is in E but not in any of  's. Indeed, if z is in
's. Indeed, if z is in  for some
for some  , then
, then 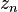 is in
is in  , a contradiction. Suppose z is in
, a contradiction. Suppose z is in  . Then
. Then  is in
is in  . If n is 2, we are done. If n > 2, then, since
. If n is 2, we are done. If n > 2, then, since  is a prime ideal, some
is a prime ideal, some  is in
is in  , a contradiction.
, a contradiction.
Notes
- ↑ Proof of the fact: suppose the vector space is a finite union of proper subspaces. Consider a finite product of linear functionals, each of which vanishes on a proper subspace that appears in the union; then it is a nonzero polynomial vanishing identically, a contradiction.
References
- Mel Hochster, Dimension theory and systems of parameters, a supplementary note