Omar Khayyam
| Omar Khayyám عمر خیام | |
|---|---|
 Omar Khayyam bust in Nishapur, Iran | |
| Born |
18 May[1] 1048[2] Nishapur, Khorasan, Persia (Iran) |
| Died |
4 December[1] 1131 (aged 83)[2] Nishapur, Khorasan, Persia (Iran) |
| Nationality | Persian |
| School | Islamic mathematics, Persian poetry, Persian philosophy |
Main interests | Mathematics, Astronomy, Philosophy, Poetry |
|
Influenced
| |
Omar Khayyám ; born Ghiyāth ad-Dīn Abu'l-Fatḥ ʿUmar ibn Ibrāhīm al-Khayyām Nīshāpūrī (/ˈoʊmɑːr kaɪˈjɑːm, -ˈjæm, ˈoʊmər/; Persian: غیاثالدین ابوالفتح عمر ابراهیم خیام نیشابورﻯ, pronounced [xæjˈjɑːm]; 18 May 1048 – 4 December 1131), was a Persian Polymath, Scholar, mathematician, astronomer, philosopher, and poet, widely considered to be one of the most influential thinkers of the Middle Ages. He wrote numerous treatises on mechanics, geography, mineralogy and astronomy.
Born in Nishapur, in northeastern Persia, at a young age he moved to Samarkand and obtained his education there. Afterwards he moved to Bukhara and became established as one of the major mathematicians and astronomers of the Islamic Golden Age. He wrote one of the most important treatises on algebra written before modern times, the Treatise on Demonstration of Problems of Algebra (1070), which includes a geometric method for solving cubic equations by intersecting a hyperbola with a circle.[3] He contributed to a calendar reform.
His significance as a philosopher and teacher, and his few remaining philosophical works, have not received the same attention as his scientific and poetic writings. Al-Zamakhshari referred to him as "the philosopher of the world". He taught the philosophy of Avicenna for decades in Nishapur.[4]
Outside Iran and Persian-speaking countries, Khayyám has influenced literature and societies through the translation of his works and popularization by other scholars. The greatest such effect was in English-speaking countries. The English scholar Thomas Hyde (1636–1703) was the first non-Persian known to have studied his works. The most influential, however, was Edward FitzGerald (1809–83),[5] who made Khayyám famous in the West through his translation and adaptations of Khayyám's quatrains (Persian: رباعیات rubāʿiyāt) in the Rubaiyat of Omar Khayyam.
Khayyám died in 1131, and is buried in the Khayyám Garden in Nishapur. The reconstruction of the tombs of Persian icons like Hafez, Saadi, Attar, Pour Sina and others were built by Reza Shah and in 1963, the Mausoleum of Omar Khayyám was reconstructed on the site by Hooshang Seyhoun.
Name
غیاث الدین Ghiyāth ad-Din – means "the Shoulder of the Faith" and implies the knowledge of the Quran.
ابوالفتح عمر بن ابراهیم Abu Fat'h 'Umar bin Ibrahim – Abu means father, Fat'h means conqueror, 'Umar means life, bin means son of, Ibrahim is his father's name.
خیام Khayyām – means "tent maker", a byname from the father's craft.
نیشابورﻯ Nīshāpūrī means "of Nishapur".
Early life
Ghiyāth ad-Din Abu'l-Fat'h 'Umar ibn Ibrāhīm al-Khayyām Nīshāpūrī (Persian: غیاث الدین ابو الفتح عمر ابراهیم خیام نیشاپوری) was born in Nishapur, then a Seljuq capital in Khorasan,[6][7][8] rivalling Cairo or Baghdad. He was born into a family of tent-makers (Khayyám), and on this name later in life:
Khayyám, who stitched the tents of science,
Has fallen in grief's furnace and been suddenly burned,
The shears of Fate have cut the tent ropes of his life,
And the broker of Hope has sold him for nothing!— Omar Khayyám[3]
He spent part of his childhood in the town of Balkh (in present-day northern Afghanistan), studying under the scholar Sheikh Muhammad Mansuri. He later studied under Imam Mowaffaq Nishapuri, one of the greatest teachers of the Khorasan region. Throughout his life, Omar Khayyám taught algebra and geometry during the day, and in the evening attended the Seljuq court as an adviser of Malik-Shah I.[9] At night he studied astronomy and worked on the Jalali calendar.
Khayyám's years in Isfahan were productive, but after the death of the Seljuq Sultan Malik-Shah I (presumably by the Assassins' sect), the Sultan's widow turned against him as an adviser, and as a result, he soon set out on his Hajj or pilgrimage to Mecca and Medina. He was then allowed to work as a court astrologer, and to return to Nishapur.[1]
Mathematician
Khayyám was famous during his life as a mathematician. He wrote the influential Treatise on Demonstration of Problems of Algebra (1070), which laid down the principles of algebra later adopted in Europe. In particular, he derived general methods for solving cubic equations, and for some equations of higher order.

In the Treatise, he wrote on the triangular array of binomial coefficients known as Pascal's triangle. In 1077, Khayyám wrote Sharh ma ashkala min musadarat kitab Uqlidis (Explanations of the Difficulties in the Postulates of Euclid) published in English as "On the Difficulties of Euclid's Definitions".[10] An important part of the book is concerned with Euclid's famous parallel postulate, which attracted the interest of Thabit ibn Qurra. Al-Haytham had previously attempted a demonstration of the postulate; Khayyám's attempt was a distinct advance, and his criticisms made their way to Europe, and may have contributed to the eventual development of non-Euclidean geometry.
Khayyám wrote on geometry, specifically on the theory of proportions.[11]
Theory of parallels

Khayyám wrote Explanations of the difficulties in the postulates in Euclid's Elements. The book consists of several sections on the parallel postulate (Book I), on the Euclidean definition of ratios and the Anthyphairetic ratio (modern continued fractions) (Book II), and on the multiplication of ratios (Book III).
The first section is a treatise containing some propositions and lemmas concerning the parallel postulate. It has reached the Western world from a reproduction in a manuscript written in 1387–88 by the Persian mathematician Tusi. Tusi mentions explicitly that he re-writes the treatise "in Khayyám's own words" and quotes Khayyám, saying that "they are worth adding to Euclid's Elements (first book) after Proposition 28."[12] This proposition[13] states a condition enough for having two lines in plane parallel to one another. After this proposition follows another, numbered 29, which is converse to the previous one.[14] The proof of Euclid uses the so-called parallel postulate (numbered 5). Objection to the use of parallel postulate and alternative view of proposition 29 have been a major problem in foundation of what is now called non-Euclidean geometry.
The treatise of Khayyám can be considered the first treatment of the parallels axiom not based on petitio principii, but on a more intuitive postulate. Khayyám refutes the previous attempts by other Greek and Persian mathematicians to prove the proposition. And he, as Aristotle, refuses the use of motion in geometry and therefore dismisses the different attempt by Ibn Haytham too.[15] In a sense he made the first attempt at formulating a non-Euclidean postulate as an alternative to the parallel postulate,[16]
Geometric algebra
Omar Khayyam[17]

This philosophical view of mathematics (see below) has influenced Khayyám's celebrated approach and method in geometric algebra and in particular in solving cubic equations. His solution is not a direct path to a numerical solution, and his solutions are not numbers but line segments. Khayyám's work can be considered the first systematic study and the first exact method of solving cubic equations.[18]
In an untitled writing on cubic equations by Khayyám discovered in the 20th century,[17] where the above quote appears, Khayyám works on problems of geometric algebra. First is the problem of "finding a point on a quadrant of a circle such that when a normal is dropped from the point to one of the bounding radii, the ratio of the normal's length to that of the radius equals the ratio of the segments determined by the foot of the normal." Again in solving this problem, he reduces it to another geometric problem: "find a right triangle having the property that the hypotenuse equals the sum of one leg (i.e. side) plus the altitude on the hypotenuse ".[19] To solve this geometric problem, he specializes a parameter and reaches the cubic equation x3 + 200x = 20x2 + 2000.[17] Indeed, he finds a positive root for this equation by intersecting a hyperbola with a circle.
This particular geometric solution of cubic equations has been further investigated and extended to degree four equations.[20]
Regarding more general equations he states that the solution of cubic equations requires the use of conic sections and that it cannot be solved by ruler and compass methods.[17] A proof of this impossibility was only plausible 750 years after Khayyám died. In this paper Khayyám mentions his will to prepare a paper giving full solution to cubic equations: "If the opportunity arises and I can succeed, I shall give all these fourteen forms with all their branches and cases, and how to distinguish whatever is possible or impossible so that a paper, containing elements which are greatly useful in this art, will be prepared."[17]
This refers to the book Treatise on Demonstrations of Problems of Algebra (1070), which laid down the principles of algebra, part of the body of Persian mathematics that was eventually transmitted to Europe.[18] In particular, he derived general methods for solving cubic equations and even some higher orders.
Binomial theorem and extraction of roots
From the Indians one has methods for obtaining square and cube roots, methods based on knowledge of individual cases—namely the knowledge of the squares of the nine digits 12, 22, 32 (etc.) and their respective products, i.e. 2 × 3 etc. We have written a treatise on the proof of the validity of those methods and that they satisfy the conditions. In addition we have increased their types, namely in the form of the determination of the fourth, fifth, sixth roots up to any desired degree. No one preceded us in this and those proofs are purely arithmetic, founded on the arithmetic of The Elements.
Omar Khayyam Treatise on Demonstration of Problems of Algebra[21]
This particular remark of Khayyám and certain propositions found in his Algebra book have made some historians of mathematics believe that Khayyám had indeed a binomial theorem up to any power. The case of power 2 is explicitly stated in Euclid's elements and the case of at most power 3 had been established by Indian mathematicians. Khayyám was the mathematician who noticed the importance of a general binomial theorem. The argument supporting the claim that Khayyám had a general binomial theorem is based on his ability to extract roots.[22]
Khayyám-Saccheri quadrilateral
The Saccheri quadrilateral was first considered by Khayyám in the late 11th century in Book I of Explanations of the Difficulties in the Postulates of Euclid.[23] Unlike many commentators on Euclid before and after him (including of course Saccheri), Khayyám was not trying to prove the parallel postulate as such but to derive it from an equivalent postulate he formulated from "the principles of the Philosopher" (Aristotle):
- Two convergent straight lines intersect and it is impossible for two convergent straight lines to diverge in the direction in which they converge.[24]
Khayyám then considered the three cases (right, obtuse and acute) that the summit angles of a Saccheri quadrilateral can take and after proving a number of theorems about them, he (correctly) refuted the obtuse and acute cases based on his postulate and hence derived the classic postulate of Euclid.
It wasn't until 600 years later that Giordano Vitale made an advance on Khayyám in his book Euclide restituo (1680, 1686), when he used the quadrilateral to prove that if three points are equidistant on the base AB and the summit CD, then AB and CD are everywhere equidistant. Saccheri himself based the whole of his long, heroic, and ultimately flawed proof of the parallel postulate around the quadrilateral and its three cases, proving many theorems about its properties along the way.
Astronomer
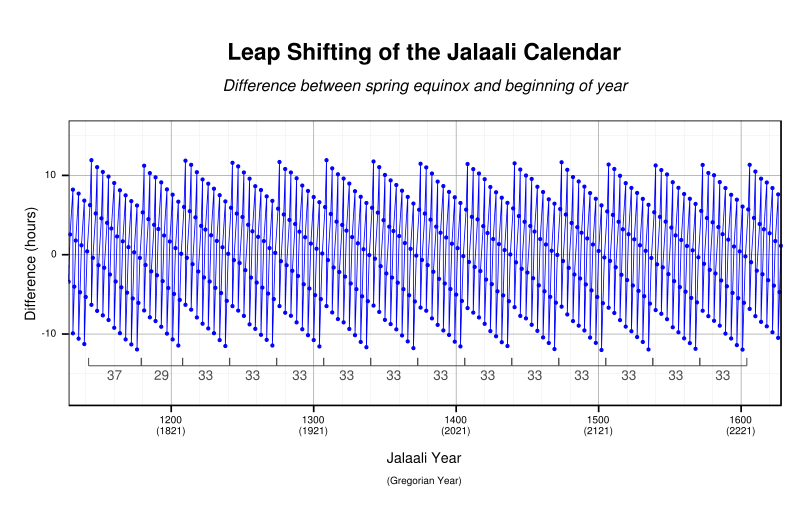
Like most Persian mathematicians of the period, Khayyám was also an astronomer and achieved fame in that role. In 1073, the Seljuq Sultan Jalal al-Din Malik-Shah Saljuqi (Malik-Shah I, 1072–92), invited Khayyám to build an observatory, along with various other distinguished scientists. According to some accounts, the version of the medieval Iranian calendar in which 2,820 solar years together contain 1,029,983 days (or 683 leap years, for an average year length of 365.24219858156 days) was based on the measurements of Khayyám and his colleagues.[29] Another proposal is that Khayyám's calendar simply contained eight leap days every thirty-three years (for a year length of 365.2424 days).[30] In either case, his calendar was more accurate to the mean tropical year than the Gregorian calendar of 500 years later. The modern Iranian calendar is based on his calculations.
Heliocentric theory
It is sometimes claimed that Khayyám demonstrated that the earth rotates on its axis[31] by presenting a model of the stars to his contemporary al-Ghazali in a planetarium.[32]
The other source for the claim that Khayyám believed in heliocentrism is Edward FitzGerald's popular but anachronistic rendering[33] of Khayyam's poetry, in which the first lines are mistranslated with a heliocentric image of the Sun flinging "the Stone that puts the Stars to Flight".[34]
Calendar reform
Khayyám was a member of a panel that reformed the Iranian calendar. The panel was convened by Seljuk Sultan Malik Shah I, and completed its reforms in 1079, resulting in the Jalali calendar.[35][36]
The Jalali calendar remained in use across Greater Iran from the 11th to the 20th centuries. It is the basis of the Iranian calendar, which is followed today in Iran and Afghanistan. While the Jalali calendar is more accurate than the Gregorian, it is based on actual solar transit, similar to Hindu calendars, and requires an ephemeris for calculating dates. The lengths of the months can vary between 29 and 31 days depending on the moment when the sun crosses into a new zodiacal area (an attribute common to most Hindu calendars). This meant that seasonal errors were lower than in the Gregorian calendar.
The modern-day Iranian calendar standardizes the month lengths based on a reform from 1925, thus minimizing the effect of solar transits. Seasonal errors are somewhat higher than in the Jalali version, but leap years are calculated as before.
Poetry

Scholars believe he wrote about a thousand four-line verses or rubaiyat. He was introduced to the English-speaking world through the Rubáiyát of Omar Khayyám, which are poetic, rather than literal, translations by Edward FitzGerald (1809–1883). Other English translations of parts of the rubáiyát (rubáiyát meaning "quatrains") exist, but FitzGerald's are the most well known.

Ironically, FitzGerald's translations reintroduced Khayyám to Iranians "who had long ignored the Neishapouri poet". A 1934 book by one of Iran's most prominent writers, Sadeq Hedayat, Songs of Khayyám (Taranehha-ye Khayyám), is said to have "shaped the way a generation of Iranians viewed" the poet.[37]
Omar Khayyám's poems have been translated into many languages.[38] Many translations were made directly from Persian, more literal than the translation by Edward Fitzgerald.[38] The following samples are from FitzGerald's translation.
The Moving Finger writes; and, having writ,
Moves on: nor all thy Piety nor Wit,
Shall lure it back to cancel half a Line,
Nor all thy Tears wash out a Word of it.But helpless pieces in the game He plays,
Upon this chequer-board of Nights and Days,
He hither and thither moves, and checks… and slays,
Then one by one, back in the Closet lays.And, as the Cock crew, those who stood before
The Tavern shouted— “Open then the Door!
You know how little time we have to stay,
And once departed, may return no more.”A Book of Verses underneath the Bough,
A Jug of Wine, a Loaf of Bread—and Thou,
Beside me singing in the Wilderness,
And oh, Wilderness is Paradise enow.Myself when young did eagerly frequent
Doctor and Saint, and heard great Argument
About it and about: but evermore
Came out of the same Door as in I went.With them the Seed of Wisdom did I sow,
And with my own hand labour’d it to grow:
And this was all the Harvest that I reap’d—
“I came like Water, and like Wind I go.”Into this Universe, and why not knowing,
Nor whence, like Water willy-nilly flowing:
And out of it, as Wind along the Waste,
I know not whither, willy-nilly blowing.And that inverted Bowl we call The Sky,
Whereunder crawling coop’t we live and die,
Lift not thy hands to It for help—for It
Rolls impotently on as Thou or I.I sent my Soul through the Invisible,
Some letter of that After-life to spell:
And by and by my Soul return'd to me,
And answer'd "I Myself am Heav'n and Hell:"
Views on religion
There have been widely divergent views on Khayyám. At one end of the spectrum, there are nightclubs named after Khayyám, and he is seen as an agnostic hedonist.[39] On the other end of the spectrum, he is seen as a mystical Sufi Muslim poet with a complex set of ideals.
- As a Skeptic

Christopher Hitchens, for instance, identifies Khayyám as a skeptic, whose poetry was satirizing the claims and practices of religion.[40]
Sadegh Hedayat states in his introductory essay to his second edition of the Quatrains of the Philosopher Omar Khayyám that "while Khayyám believes in the transmutation and transformation of the human body, he does not believe in a separate soul; if we are lucky, our bodily particles would be used in the making of a jug of wine".[41] He further maintains that Khayyam's meaning of "wine" is literal, and different from Sufi's usage of wine.
FitzGerald, in his preface to the Rubáiyát, also contested claims that Khayyám was a Sufi mystic:
| “ | Omar's Epicurean Audacity of thought and Speech caused him to be regarded askance in his own time and country. He is said to have been especially hated and dreaded by the Sufis, whose practice he ridiculed, and whose faith amounts to little more than his own, when stripped of the Mysticism and formal recognition of Islamism under which Omar would not hide.[42] | ” |
- As a Sufi Muslim
Omar Khayyam revered Prophet Muhammad as demonstrated by his writings. In his book entitled On the elaboration of the problems concerning the book of Euclid he refers to the Prophet Muhammad as "master of prophets."[43] In the same book, Khayyam at the end of it affirms what he stated and praises God and Prophet Muhammad.[43] In his piece entitled On Existence Khayyam refers to Prophet Muhammad as his master.[44] In his Quatrains, Khayyam asks Prophet Muhammad to admit him into heaven.[45] Khayyam states about the Prophet:
O Thou! to please whose love and wrath as well,
Allah created heaven and likewise hell;
Thou hast thy court in heaven, and I have naught,
Why not admit me in thy courts to dwell?[1]
- ^ Cite error: The named reference
quatrainswas invoked but never defined (see the help page).
Islamic Philosopher Seyyed Hossein Nasr maintains that it is reductive to establish Khayyam's personal views about God or religion based on a literal interpretation of his poems (many of which are also apocryphal) because he elsewhere wrote a treatise entitled "al-Khutbat al-gharrå˘" (The Splendid Sermon) on the praise of God, where he holds orthodox views, agreeing with Avicenna on Divine Unity.[4] Furthermore, Khayyam's most important single philosophical work is al-Risālah fil-wujūd (الرسالة في الوجود, "Treatise on Being"), written in Arabic, which begins with Quranic verses and asserts that all things come from God and that there is an order to all things.[4]
C.H.A. Bjerregaard has a similar take on the issue:
"The writings of Omar Khayyam are good specimens of Sufism, but are not valued in the West as they ought to be, and the mass of English-speaking people know him only through the poems of Edward Fitzgerald. It is unfortunate because Fitzgerald is not faithful to his master and model, and at times he lays words upon the tongue of the Sufi which are blasphemous. Such outrageous language is that of the eighty-first quatrain for instance. Fitzgerald is doubly guilty because he was more of a Sufi than he was willing to admit."[46]
A French orientalist named Franz Toussaint, dissatisfied with Fitzgerald's translation wrote his own directly from the Persian text, claiming to express the spirit of the verses rather than to versify.[47] His translation was published by Editions d'Art Henri Piazza.
Abdullah Dougan, a modern Naqshbandi Sufi, provides commentary[48] on the role and contribution of Omar Khayyam to Sufi thought. Dougan says that while Omar is a minor Sufi teacher compared to the giants – Rumi, Attar and Sana’i – one aspect that makes Omar’s work so relevant and accessible is its very human scale as we can feel for him and understand his approach. The argument over the quality of Fitzgerald’s translation of the Rubaiyat has, according to Dougan, diverted attention from a fuller understanding of the deeply esoteric message contained in Omar’s actual material – "Every line of the Rubaiyat has more meaning than almost anything you could read in Sufi literature".
Philosopher
Khayyám himself rejected any association with the title falsafī "philosopher" in the sense of Aristotelianism and stressed he wishes "to know who I am". In the context of philosophers he was labeled by some of his contemporaries as "detached from divine blessings".[49]
It is now established that Khayyám taught for decades the philosophy of Avicena, especially the Book of Healing, in his home town Nishapur, till his death.[4] In an incident he had been requested to comment on a disagreement between Avicena and a philosopher called Abu'l-Barakāt al-Baghdādī who had criticized Avicena strongly. Khayyám is said to have answered "[he] does not even understand the sense of the words of Avicenna, how can he oppose what he does not know?"[49]
Khayyám the philosopher could be understood from two rather distinct sources. One is through his Rubaiyat and the other through his own works in light of the intellectual and social conditions of his time.[50] The latter could be informed by the evaluations of Khayyám's works by scholars and philosophers such as Abul-Fazl Bayhaqi, Nizami Aruzi, and al-Zamakhshari and Sufi poets and writers Attar of Nishapur and Najm-al-Din Razi.
Mathematical philosophy
As a mathematician, Khayyám has made fundamental contributions to the philosophy of mathematics especially in the context of Persian Mathematics and Persian philosophy with which most of the other Persian scientists and philosophers such as Avicenna, Abū Rayḥān al-Bīrūnī and Tusi are associated. There are at least three basic mathematical ideas of strong philosophical dimensions that can be associated with Khayyám.
- Mathematical order: From where does this order issue, and why does it correspond to the world of nature? His answer is in one of his philosophical "treatises on being". Khayyám's answer is that "the Divine Origin of all existence not only emanates wujud "being", by virtue of which all things gain reality, but It is the source of order that is inseparable from the very act of existence."[50]
- The significance of axioms in geometry and the necessity for the mathematician to rely upon philosophy and hence the importance of the relation of any particular science to prime philosophy. This is the philosophical background to Khayyám's total rejection of any attempt to "prove" the parallel postulate, and in turn his refusal to bring motion into the attempt to prove this postulate, as had Ibn al-Haytham, because Khayyám associated motion with the world of matter, and wanted to keep it away from the purely intelligible and immaterial world of geometry.[50]
- Clear distinction made by Khayyám, on the basis of the work of earlier Persian philosophers such as Avicenna, between natural bodies and mathematical bodies. The first is defined as a body that is in the category of substance and that stands by itself, and hence a subject of natural sciences, while the second, called "volume", is of the category of accidents (attributes) that do not subsist by themselves in the external world and hence is the concern of mathematics. Khayyám was very careful to respect the boundaries of each discipline, and criticized Ibn al-Haytham in his proof of the parallel postulate precisely because he had broken this rule and had brought a subject belonging to natural philosophy, that is, motion, which belongs to natural bodies, into the domain of geometry, which deals with mathematical bodies.[50]
Gallery
-

Persian: "این قافلهٔ عُمر عجب میگذرد" — A line of poetry by the Iranian poet Omar Khayyam in Shikasta Nastaʿlīq.
-

A ruba'i of Omar Khayyam in Shikasta Nastaʿlīq calligraphy.
Legacy
A lunar crater Omar Khayyam was named after him in 1970 and a minor planet called 3095 Omarkhayyam, discovered by Soviet astronomer Lyudmila Zhuravlyova in 1980, is named after him.[51]
In June 2009 Iran donated a scholar pavilion to United Nations Office in Vienna which is placed in the central Memorial Plaza of the Vienna International Center.[52] The Persian Scholars Pavilion at United Nations in Vienna, Austria is featuring the statues of four prominent Iranian figures. Highlighting the Iranian architectural features, the pavilion is adorned with Persian art forms and includes the statues of renowned Iranian scientists Avicenna, Abu Rayhan Biruni, Zakariya Razi (Rhazes) and Omar Khayyam.[53][54]
.jpg)
In March 2016, Khayyam's statue was unveiled by in the courtyard of the university of Oklahoma as well. In addition, two other copies of the statue, one of which was installed in Khayyam’s hometown of Neyshabur, and the other is to be sent to Florence, Italy. The three statues were created by Iranian sculptor Hossein Fakhimi. The President of the University of Oklahoma David L. Boren, a former governor of Oklahoma and U.S. senator, also attended the ceremony. The ceremony was organized with the help of the International Society for Iranian Culture.[55][56]
.jpg)
One of the founders of the Discordian religion, Omar Khayyam Ravenhurst named himself after the figure.
See also
- Astronomy in medieval Islam
- Mathematics in medieval Islam
- Nozhat al-Majales
- Omar Khayyam (film)
- The Keeper: The Legend of Omar Khayyam
Notes
- 1 2 3 "Omar Khayyam (Persian poet and astronomer)". Britannica.com. Retrieved 2012-05-30.
- 1 2 Professor Seyyed Hossein Nasr and Professor Mehdi Aminrazavi. “An Anthology of Philosophy in Persia, Vol. 1: From Zoroaster to ‘Umar Khayyam”, I.B. Tauris in association with The Institute of Ismaili Studies, 2007.
- 1 2 "Omar Khayyam". The MacTutor History of Mathematics archive.
- 1 2 3 4 S. H. Nasr, 2006, Islamic Philosophy from Its Origin to the Present, Chapter 9., pp. 165–183
- ↑ Jos Biegstraaten
- ↑ The Tomb of Omar Khayyâm, George Sarton, Isis, Vol. 29, No. 1 (Jul., 1938), 15.
- ↑ Edward FitzGerald, Rubaiyat of Omar Khayyam, Ed. Christopher Decker, (University of Virginia Press, 1997), xv;"The Saljuq Turks had invaded the province of Khorasan in the 1030s, and the city of Nishapur surrendered to them voluntarily in 1038. Thus Omar Khayyam grew to maturity during the first of the several alien dynasties that would rule Iran until the twentieth century.".
- ↑ Peter Avery and John Heath-Stubbs, The Ruba'iyat of Omar Khayyam, (Penguin Group, 1981), 14;"These dates, 1048-1031, tell us that Khayyam lived when the Saljuq Turkish Sultans were extending and consolidating their power over Persia and when the effects of this power were particularly felt in Nishapur, Khayyam's birthplace.".
- ↑ Edward FitzGerald, Rubaiyat of Omar Khayyam, xv.
- ↑ The Quatrains of Omar Khayyam E.H. Whinfield Pg 14
- ↑ "FSTC Newsletter, Issue 8: "The Isfizari Project"". Muslimheritage.com. 2011-11-11. Retrieved 2012-05-30.
- ↑ (Smith 1935, p. 6)
- ↑ Euclid. "Proposition 28". Elements. I. 28.
If a straight line falling on two straight lines make the exterior angle equal to the interior and opposite angle on the same side, or the interior angles on the same side equal to two right angles, the straight lines will be parallel to one another.
- ↑ Euclid. "Proposition 29". Elements. I. 29.
A straight line falling on parallel straight lines makes the alternate angles equal to one another, the exterior angle equal to the interior and opposite angle, and the interior angles on the same side equal to two right angles.
- ↑ (Rozenfeld 1988, pp. 64–65)
- ↑ (Katz 1998, p. 270). Excerpt: In some sense, his treatment was better than ibn al-Haytham's because he explicitly formulated a new postulate to replace Euclid's rather than have the latter hidden in a new definition.
- 1 2 3 4 5 A. R. Amir-Moez, "A Paper of Omar Khayyám", Scripta Mathematica 26 (1963), pp. 323–37
- 1 2 Mathematical Masterpieces: Further Chronicles by the Explorers, p. 92
- ↑ E. S. Kennedy, Chapter 10 in Cambridge History of Iran (5), p. 665.
- ↑ A. R. Amir-Moez, Khayyam's Solution of Cubic Equations, Mathematics Magazine, Vol. 35, No. 5 (Nov., 1962), pp. 269–271. This paper contains an extension by the late Mohsen Hashtroodi of Khayyám's method to degree four equations.
- ↑ "Muslim extraction of roots". Mactutor History of Mathematics.
- ↑ J. L. Coolidge, The Story of the Binomial Theorem, Amer. Math. Monthly, Vol. 56, No. 3 (Mar., 1949), pp. 147–157
- ↑ Boris Abramovich Rozenfelʹd (1988), A History of Non-Euclidean Geometry: Evolution of the Concept of a Geometric Space, p. 65. Springer, ISBN 0-387-96458-4.
- ↑ Boris A Rosenfeld and Adolf P Youschkevitch (1996), Geometry, p.467 in Roshdi Rashed, Régis Morelon (1996), Encyclopedia of the history of Arabic science, Routledge, ISBN 0-415-12411-5.
- ↑ دقیق ترین تقویم جهان، هدیه خیام به ایرانیان (in Persian). Bbc.co.uk. Retrieved 2012-05-30.
- ↑ پيمانه کردن سال و ماه از ديرباز تا کنون در گفتگو با دکتر ايرج ملک پور (in Persian). Bbc.co.uk. Retrieved 2012-05-30.
- ↑ پژوهشهای ایرانی | پاسداشت گاهشماری ایرانی (in Persian). Ghiasabadi.com. Retrieved 2012-05-30.
- ↑ پژوهشهای ایرانی | گاهشماری تقویم جلالی (in Persian). Ghiasabadi.com. Retrieved 2012-05-30.
- ↑ "Early History of Astronomy – The Middle East". Ephemeris.com. Retrieved 2012-09-08.
- ↑ Mapping Time: The Calendar and its History by E.G. Richards (Oxford University Press, 1998) ISBN 978-0-19-286205-1, p. 235
- ↑ "physicsoftheuniverse.com". physicsoftheuniverse.com. Retrieved 2012-09-08.
- ↑ "Theory". Khayyam.info. Retrieved 2012-09-08.
- ↑ Donald and Marilynn Olson (1988), 'Zodiac Light, False Dawn, and Omar Khayyam', The Observatory, vol. 108, p. 181-182
- ↑ "Rex Pay, 2000". Humanistictexts.org. Retrieved 2012-09-08.
- ↑ Farrell, Charlotte (1996), "The ninth-century renaissance in astronomy", The Physics Teacher, 34: 268–272, doi:10.1119/1.2344432.
- ↑ Struik, D. J. (1958), "Omar Khayyam, mathematician", The Mathematics Teacher, 51 (4): 280–285, JSTOR 27955652.
- ↑ Molavi, Afshin, The Soul of Iran, Norton, (2005), p.110
- 1 2 The Great Umar Khayyam: A Global Reception of the Rubaiyat (AUP – Leiden University Press) by A. A. Seyed-Gohrab, 2012.
- ↑ Sadegh Hedayat pointed out that Khayyám, "from his youth to his death, remained a materialist, pessimist, agnostic". "Khayyám looked at all religions' questions with a skeptical eye", continues Hedayat, "and hated the fanaticism, narrow-mindedness, and the spirit of vengeance of the mullahs, the so-called religious scholars".
- ↑ Hitchens, C. (2007). The portable atheist: Essential readings for the nonbeliever (p. 7). Philadelphia, PA: Da Capo.
- ↑ Katouzian, H. (1991). Sadeq Hedayat: The life and literature of an Iranian writer (p. 138). London: I.B. Tauris
- ↑ FitzGerald, E. (2010). Rubaiyat of Omar Khayyam (p. 12). Champaign, Ill.: Project Gutenberg
- 1 2 Mehdi Aminrazavi (2005), The Wine of Wisdom: The Life, Poetry and Philosophy of Omar Khayyam, Oneworld Publications, p. 55, ISBN 978 1-85168-504-2
- ↑ Mehdi Aminrazavi (2005), p.56
- ↑ The Sufistic Quatrains of Omar Khayyam, New York M.W. Dunne, 1903, p. 145
- ↑ C. H. A. Bjerregaard (1915). Sufism: Omar Khayyam and E. Fitzgerald. The Sufi Publishing Society. Preface.
- ↑ "Robaiyat - Wikilivres".
- ↑ Abdullah Dougan Who is the Potter? Gnostic Press 1991 ISBN 0-473-01064-X
- 1 2 Bausani, A., Chapter 3 in Cambridge History of Iran (5), p. 289.
- 1 2 3 4 S. H. Nasr Chapter 9, p . 170-1
- ↑ Dictionary of Minor Planet Names – p.255. Books.google.com. 1979-02-26. Retrieved 2012-09-08.
- ↑ UNIS. "Monument to Be Inaugurated at the Vienna International Centre, 'Scholars Pavilion' donated to International Organizations in Vienna by Iran".
- ↑ "The Monument donated by the Islamic Republic of Iran to the International Organization in Vienna". Permanent Mission of the Islamic Republic of Iran to the United Nations Office - Vienna.
- ↑ Hosseini, Mir Masood. "Negareh: Persian Scholars Pavilion at United Nations Vienna, Austria".
- ↑ "Khayyam statue finally set up at University of Oklahoma". Tehran Times. Retrieved 2016-04-04.
- ↑ "University of Oklahoma to establish Center for Iranian and Persian Gulf Studies". NewsOK.com. Retrieved 2016-04-04.
References
- Turner, Howard R. (1997). Science in Medieval Islam: An Illustrated Introduction. University of Texas Press. ISBN 0-292-78149-0.
- Jos Biegstraaten (2008). "Omar Khayyam (His impact on the literary and social scene abroad)". Encyclopaedia Iranica. vol. 15. Encyclopaedia Iranica Foundation.
- Nasr, S. H. (2006). Islamic Philosophy from Its Origin to the Present: Philosophy in the Land of Prophecy. SUNY Press. ISBN 0-7914-6799-6.
- Katz, Victor (1998). A History of Mathematics: An Introduction (2 ed.). Addison-Wesley. p. 879. ISBN 0-321-01618-1.
- KnoebelNasr, Arthur; Laubenbacher, Reinhard; Lodder, Jerry; Pengelley, David (2007). Mathematical Masterpieces: Further Chronicles by the Explorers. Springer. ISBN 0-387-33061-5.
- ed. by J.A. Boyle. (1968). The Cambridge History of Iran (5): The Saljug and Mongol Periods. Cambridge University Press. ISBN 0-521-06936-X.
- Smith, David Eugene (1935). "Euclid, Omar Khayyâm, and Saccheri". Scripta Mathematica. III (1): 5–10. OCLC 14156259.
- Rozenfeld, Boris A. (1988). A History of Non-Euclidean Geometry: Evolution of the Concept of a Geometric Space. Springer Verlag. pp. 65, 471. ISBN 0-387-96458-4.
- E.G. Browne (1998). Literary History of Persia. (Four volumes, 2,256 pages, and 25 years in the writing). ISBN 0-7007-0406-X
- Jan Rypka (1968). History of Iranian Literature. Reidel Publishing Company. OCLC 460598. ISBN 90-277-0143-1
- Omar Khayyam: Vierzeiler (Rubāʿīyāt) übersetzt von Friedrich Rosen mit Miniaturen von Hossein Behzad. ISBN 978-3-86931-622-2 Details
For Further Reference:
- R. M. Chopra, "Great Poets of Classical Persian", June 2014, Sparrow Publication, Kolkata. (ISBN 978-81-89140-99-1).
External links
| Wikiquote has quotations related to: Omar Khayyam |
| Wikimedia Commons has media related to Omar Khayyam. |
- Hashemipour, Behnaz (2007). "Khayyām: Ghiyāth al‐Dīn Abū al‐Fatḥ ʿUmar ibn Ibrāhīm al‐Khayyāmī al‐Nīshāpūrī". In Thomas Hockey; et al. The Biographical Encyclopedia of Astronomers. New York: Springer. pp. 627–8. ISBN 978-0-387-31022-0. (PDF version)
- Umar Khayyam, at the Stanford Encyclopedia of Philosophy
- Khayyam's works in original Persian at Ganjoor Persian Library
- Khayyam in Tarikhema.ir
- Works by Omar Khayyam at Project Gutenberg
- Works by or about Omar Khayyam at Internet Archive
- Works by Omar Khayyam at LibriVox (public domain audiobooks)

- The illustrated Rubáiyát of Omar Khayyám at Internet Archive.
- Omar Khayyam's Rubaiyat as translated by Edward Fitzgerald – 1st edition
- The Rubaiyat by Omar Khayyam – The Internet Classics Archive
- Illustrations to the Rubaiyat by Adelaide Hanscom
- Panoramic Images of Khayyam’s Tomb Neyshabur Day