Method of exhaustion
The method of exhaustion (methodus exhaustionibus, or méthode des anciens) is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the n-th polygon and the containing shape will become arbitrarily small as n becomes large. As this difference becomes arbitrarily small, the possible values for the area of the shape are systematically "exhausted" by the lower bound areas successively established by the sequence members.
The method of exhaustion typically required a form of proof by contradiction, known as reductio ad absurdum. This amounts to finding an area of a region by first comparing it to the area of a second region (which can be “exhausted” so that its area becomes arbitrarily close to the true area). The proof involves assuming that the true area is greater than the second area, and then proving that assertion false, and then assuming that it is less than the second area, and proving that assertion false, too.
History
.jpg)
The idea originated in the late 5th century BC with Antiphon, although it is not entirely clear how well he understood it.[1] The theory was made rigorous a few decades later by Eudoxus of Cnidus, who used it to calculate areas and volumes. It was later reinvented in China by Liu Hui in the 3rd century AD in order to find the area of a circle.[2] The first use of the term was in 1647 by Grégoire de Saint-Vincent in Opus geometricum quadraturae circuli et sectionum.
The method of exhaustion is seen as a precursor to the methods of calculus. The development of analytical geometry and rigorous integral calculus in the 17th-19th centuries subsumed the method of exhaustion so that it is no longer explicitly used to solve problems. An important alternative approach was Cavalieri's principle, also termed the "method of indivisibles", which eventually evolved into the infinitesimal calculus of Roberval, Torricelli, Wallis, Leibniz, and others.
Euclid
Euclid used the method of exhaustion to prove the following six propositions in the book 12 of his Elements.
- Proposition 2
- The area of a circle is proportional to the square of its radius.
- Proposition 5
- The volumes of two tetrahedra of the same height are proportional to the areas of their triangular bases.
- Proposition 10
- The volume of a cone is a third of the volume of the corresponding cylinder which has the same base and height.
- Proposition 11
- The volume of a cone (or cylinder) of the same height is proportional to the area of the base.
- Proposition 12
- The volume of a cone (or cylinder) that is the similar to another is proportional to the cube of the ratio of the diameters of the bases.
- Proposition 18
- The volume of a sphere is proportional to the cube of its diameter.
Archimedes
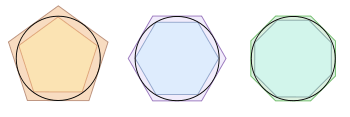
Archimedes used the method of exhaustion as a way to compute the area inside a circle by filling the circle with a polygon of a greater area and greater number of sides. The quotient formed by the area of this polygon divided by the square of the circle radius can be made arbitrarily close to π as the number of polygon sides becomes large, proving that the area inside the circle of radius r is πr2, π being defined as the ratio of the circumference to the diameter (C/d) or of the area of the circle to the square of its radius (A/r²).
He also provided the bounds 3 + 10/71 < π < 3 + 10/70, (giving a range of 1/497) by comparing the perimeters of the circle with the perimeters of the inscribed and circumscribed 96-sided regular polygons.
Other results he obtained with the method of exhaustion included[3]
- The area bounded by the intersection of a line and a parabola is 4/3 that of the triangle having the same base and height;
- The area of an ellipse is proportional to a rectangle having sides equal to its major and minor axes;
- The volume of a sphere is 4 times that of a cone having a base and height of the same radius;
- The volume of a cylinder having a height equal to its diameter is 3/2 that of a sphere having the same diameter;
- The area bounded by one spiral rotation and a line is 1/3 that of the circle having a radius equal to the line segment length;
- Use of the method of exhaustion also led to the successful evaluation of an infinite geometric series (for the first time).
See also
Notes and references
- ↑ The MacTutor History of Mathematics archive
- ↑ Dun, Liu; Fan, Dainian; Cohen, Robert Sonné (1966). "A comparison of Archimdes' and Liu Hui's studies of circles". Chinese studies in the history and philosophy of science and technology. 130. Springer: 279. ISBN 0-7923-3463-9., Chapter , p. 279
- ↑ Smith, David E (1958). History of Mathematics. New York: Dover Publications. ISBN 0-486-20430-8.