Major sixth
| Inverse | minor third |
|---|---|
| Name | |
| Other names | septimal major sixth, supermajor sixth, major hexachord, greater hexachord, hexachordon maius |
| Abbreviation | M6 |
| Size | |
| Semitones | 9 |
| Interval class | 3 |
| Just interval | 5:3, 12:7,[1] 27:16 |
| Cents | |
| Equal temperament | 900 |
| 24 equal temperament | 900 |
| Just intonation | 884, 933, 906 |

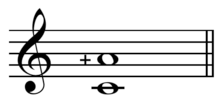
In music from Western culture, a sixth is a musical interval encompassing six note letter names or staff positions (see Interval number for more details), and the major sixth is one of two commonly occurring sixths. It is qualified as major because it is the larger of the two. The major sixth spans nine semitones. Its smaller counterpart, the minor sixth, spans eight semitones. For example, the interval from C up to the nearest A is a major sixth. It's a sixth because it encompasses six note letter names (C, D, E, F, G, A) and six staff positions. It's a major sixth, not a minor sixth, because the note A lies nine semitones above C. Diminished and augmented sixths (such as C♯ to A♭ and C to A♯) span the same number of note letter names and staff positions, but consist of a different number of semitones (seven and ten).
A commonly cited example of a melody featuring the major sixth as its opening is "My Bonnie Lies Over the Ocean".[2]
The major sixth is one of the consonances of common practice music, along with the unison, octave, perfect fifth, major and minor thirds, minor sixth and (sometimes) the perfect fourth. In the common practice period, sixths were considered interesting and dynamic consonances along with their inverses the thirds, but in medieval times they were considered dissonances unusable in a stable final sonority; however in that period they were tuned to the Pythagorean major sixth of 27/16. In just intonation, the (5/3) major sixth is classed as a consonance of the 5-limit.
A major sixth is also used in transposing music to E-flat instruments, like the alto clarinet, alto saxophone, E-flat tuba, trumpet, natural horn, and alto horn when in E-flat as a written C sounds like E-flat on those instruments.
Assuming close-position voicings for the following examples, the major sixth occurs in a first inversion minor triad, a second inversion major triad, and either inversion of a diminished triad. It also occurs in the second and third inversions of a dominant seventh chord.
The septimal major sixth (12/7) is approximated in 53 tone equal temperament by an interval of 41 steps or 928 cents.
 |
Major sixth (equal temperament)
The file plays middle C, followed by A (a tone 900 cents sharper than C), followed by both tones together. |
| Problems playing this file? See media help. | |
Frequency proportions
Many intervals in a various tuning systems qualify to be called "major sixth," sometimes with additional qualifying words in the names. The following examples are sorted by increasing width.
In just intonation, the most common major sixth is the pitch ratio of 5:3 (![]() play ), approximately 884 cents.
play ), approximately 884 cents.
In 12-tone equal temperament, a major sixth is equal to nine semitones, exactly 900 cents, with a frequency ratio of the (9/12) root of 2 over 1.
Another just major sixth is the Pythagorean major sixth[3] with a ratio of 27:16, approximately 906 cents,[4] constructed from three just perfect fifths (C-A = C-G-D-A = 702+702+702-1200=906) or by playing 27th harmonic and the next lowest octave of the fundamental frequency (16) together. The 27:16 Pythagorean major sixth arises in the C Pythagorean major scale between F and D,[5] as well as between C and A, G and E, and D and B.![]() Play
Play
The septimal major sixth (12/7) is approximated in 53-tone equal temperament by an interval of 41 steps, giving an actual frequency ratio of the (41/53) root of 2 over 1, approximately 928 cents.
Another just major sixth is the 12:7 septimal major sixth or supermajor sixth of approximately 933 cents.[4]
The nineteenth subharmonic is a major sixth, A![]() = 32/19 = 902.49 cents.
= 32/19 = 902.49 cents.
See also
Sources
- ↑ Haluska, Jan (2003). The Mathematical Theory of Tone Systems, p.xxiii. ISBN 0-8247-4714-3. Septimal major sixth.
- ↑ Neely, Blake (2009). Piano For Dummies, p.201. ISBN 0-470-49644-4.
- ↑ John Fonville. "Ben Johnston's Extended Just Intonation- A Guide for Interpreters", p.124, Perspectives of New Music, Vol. 29, No. 2 (Summer, 1991), pp. 106-137.
- 1 2 Hermann L. F Von Helmholtz (2007). On the Sensations of Tone, p.456. ISBN 978-1-60206-639-7.
- ↑ Paul, Oscar (1885). A manual of harmony for use in music-schools and seminaries and for self-instruction, p.165. Theodore Baker, trans. G. Schirmer.
Further reading
- Duckworth, William (1996). [untitled chapter] In Sound and Light: La Monte Young, Marian Zazeela, edited by William Duckworth and Richard Fleming, p. 167. Bucknell Review 40, no. 1. Lewisburg [Pa.]: Bucknell University Press; London and Cranbury, NJ: Associated University Presses. ISBN 9780838753460. Paperback reprint 2006, ISBN 0-8387-5738-3. [septimal]