Jefimenko's equations
| Electromagnetism |
|---|
 |
|
|
In electromagnetism, Jefimenko's equations (named after Oleg D. Jefimenko) describe the behavior of the electric and magnetic fields in terms of the charge and current distributions at retarded times.
Jefimenko's equations[1] are the solution of Maxwell's equations for an assigned distribution of electric charges and currents, under the assumption that there is no electromagnetic field other than the one produced by those charges and currents.
Equations
Electric and magnetic fields
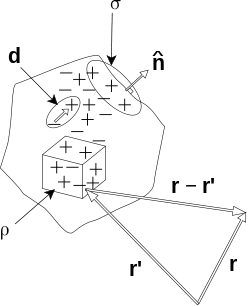
Jefimenko's equations give the E-field and B-field produced by an arbitrary charge or current distribution, of charge density ρ and current density J:[2]
where r' is a point in the charge distribution, r is a point in space, and
is the retarded time. There are similar expressions for D and H.[3]
These equations are the time-dependent generalization of Coulomb's law and the Biot–Savart law to electrodynamics, which were originally true only for electrostatic and magnetostatic fields, and steady currents.
Origin from retarded potentials
Jefimenko's equations can be found[4] from the retarded potentials φ and A:
which are the solutions to Maxwell's equations in the potential formulation, then substituting in the definitions of the electromagnetic potentials themselves
and using the relation
replaces the potentials φ and A by the fields E and B.
Discussion
There is a widespread interpretation of Maxwell's equations indicating that spatially varying electric and magnetic fields can cause each other to change in time, thus giving rise to a propagating electromagnetic wave[5] (electromagnetism). However, Jefimenko's equations show an alternative point of view.[6] Jefimenko says, "...neither Maxwell's equations nor their solutions indicate an existence of causal links between electric and magnetic fields. Therefore, we must conclude that an electromagnetic field is a dual entity always having an electric and a magnetic component simultaneously created by their common sources: time-variable electric charges and currents."[7]
As pointed out by McDonald,[8] Jefimenko's equations seem to appear first in 1962 in the second edition of Panofsky and Phillips's classic textbook.[9] Essential features of these equations are easily observed which is that the right hand sides involve "retarded" time which reflects the "causality" of the expressions. In other words, the left side of each equation is actually "caused" by the right side, unlike the normal differential expressions for Maxwell's equations where both sides take place simultaneously. In the typical expressions for Maxwell's equations there is no doubt that both sides are equal to each other, but as Jefimenko notes, "... since each of these equations connects quantities simultaneous in time, none of these equations can represent a causal relation."[10] The second feature is that the expression for E does not depend upon B and vice versa. Hence, it is impossible for E and B fields to be "creating" each other. Charge density and current density are creating them both.
See also
Notes
- ↑ Oleg D. Jefimenko, Electricity and Magnetism: An Introduction to the Theory of Electric and Magnetic Fields, Appleton-Century-Crofts (New-York - 1966). 2nd ed.: Electret Scientific (Star City - 1989), ISBN 978-0-917406-08-9. See also: David J. Griffiths, Mark A. Heald, Time-dependent generalizations of the Biot–Savart and Coulomb laws, American Journal of Physics 59 (2) (1991), 111-117.
- ↑ Introduction to Electrodynamics (3rd Edition), D.J. Griffiths, Pearson Education, Dorling Kindersley, 2007, ISBN 81-7758-293-3
- ↑ Oleg D. Jefimenko, Solutions of Maxwell's equations for electric and magnetic fields in arbitrary media, American Journal of Physics 60 (10) (1992), 899-902
- ↑ Introduction to Electrodynamics (3rd Edition), D.J. Griffiths, Pearson Education, Dorling Kindersley, 2007, ISBN 81-7758-293-3
- ↑ Kinsler, P. (2011). "How to be causal: time, spacetime, and spectra". Eur. J. Phys. 32: 1687. arXiv:1106.1792
 . Bibcode:2011EJPh...32.1687K. doi:10.1088/0143-0807/32/6/022.
. Bibcode:2011EJPh...32.1687K. doi:10.1088/0143-0807/32/6/022.
- ↑ Oleg D. Jefimenko, Causality Electromagnetic Induction and Gravitation, 2nd ed.: Electret Scientific (Star City - 2000) Chapter 1, Sec. 1-4, page 16 ISBN 0-917406-23-0.
- ↑ Oleg D. Jefimenko, Causality Electromagnetic Induction and Gravitation, 2nd ed.: Electret Scientific (Star City - 2000) Chapter 1, Sec. 1-5, page 16 ISBN 0-917406-23-0.
- ↑ Kirk T. McDonald, The relation between expressions for time-dependent electromagnetic fields given by Jefimenko and by Panofsky and Phillips, American Journal of Physics 65 (11) (1997), 1074-1076.
- ↑ Wolfgang K. H. Panofsky, Melba Phillips, Classical Electricity And Magnetism, Addison-Wesley (2nd. ed - 1962), Section 14.3. The electric field is written in a slightly different - but completely equivalent - form. Reprint: Dover Publications (2005), ISBN 978-0-486-43924-2.
- ↑ Oleg D. Jefimenko, Causality Electromagnetic Induction and Gravitation, 2nd ed.: Electret Scientific (Star City - 2000) Chapter 1, Sec. 1-1, page 6 ISBN 0-917406-23-0.