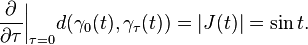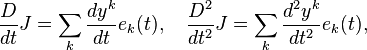Jacobi field
In Riemannian geometry, a Jacobi field is a vector field along a geodesic  in a Riemannian manifold describing the difference between the geodesic and an "infinitesimally close" geodesic. In other words, the Jacobi fields along a geodesic form the tangent space to the geodesic in the space of all geodesics. They are named after Carl Jacobi.
in a Riemannian manifold describing the difference between the geodesic and an "infinitesimally close" geodesic. In other words, the Jacobi fields along a geodesic form the tangent space to the geodesic in the space of all geodesics. They are named after Carl Jacobi.
Definitions and properties
Jacobi fields can be obtained in the following way: Take a smooth one parameter family of geodesics  with
with  , then
, then
is a Jacobi field, and describes the behavior of the geodesics in an infinitesimal neighborhood of a
given geodesic  .
.
A vector field J along a geodesic  is said to be a Jacobi field if it satisfies the Jacobi equation:
is said to be a Jacobi field if it satisfies the Jacobi equation:
where D denotes the covariant derivative with respect to the Levi-Civita connection, R the Riemann curvature tensor,  the tangent vector field, and t is the parameter of the geodesic.
On a complete Riemannian manifold, for any Jacobi field there is a family of geodesics
the tangent vector field, and t is the parameter of the geodesic.
On a complete Riemannian manifold, for any Jacobi field there is a family of geodesics  describing the field (as in the preceding paragraph).
describing the field (as in the preceding paragraph).
The Jacobi equation is a linear, second order ordinary differential equation;
in particular, values of 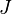 and
and  at one point of
at one point of  uniquely determine the Jacobi field. Furthermore, the set of Jacobi fields along a given geodesic forms a real vector space of dimension twice the dimension of the manifold.
uniquely determine the Jacobi field. Furthermore, the set of Jacobi fields along a given geodesic forms a real vector space of dimension twice the dimension of the manifold.
As trivial examples of Jacobi fields one can consider 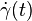 and
and 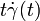 . These correspond respectively to the following families of reparametrisations:
. These correspond respectively to the following families of reparametrisations: 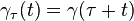 and
and 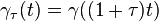 .
.
Any Jacobi field 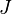 can be represented in a unique way as a sum
can be represented in a unique way as a sum  , where
, where 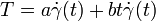 is a linear combination of trivial Jacobi fields and
is a linear combination of trivial Jacobi fields and  is orthogonal to
is orthogonal to 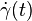 , for all
, for all  .
The field
.
The field 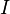 then corresponds to the same variation of geodesics as
then corresponds to the same variation of geodesics as 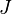 , only with changed parameterizations.
, only with changed parameterizations.
Motivating example
On a sphere, the geodesics through the North pole are great circles. Consider two such geodesics 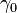 and
and  with natural parameter,
with natural parameter, ![t\in [0,\pi]](../I/m/f6beb03cafd50539f8ff9e5e3ac747ef.png) , separated by an angle
, separated by an angle  . The geodesic distance
. The geodesic distance
is
Computing this requires knowing the geodesics. The most interesting information is just that
 , for any
, for any  .
.
Instead, we can consider the derivative with respect to  at
at 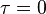 :
:
Notice that we still detect the intersection of the geodesics at  . Notice further that to calculate this derivative we do not actually need to know
. Notice further that to calculate this derivative we do not actually need to know
 ,
,
rather, all we need do is solve the equation
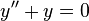 ,
,
for some given initial data.
Jacobi fields give a natural generalization of this phenomenon to arbitrary Riemannian manifolds.
Solving the Jacobi equation
Let 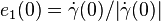 and complete this to get an orthonormal basis
and complete this to get an orthonormal basis  at
at 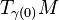 . Parallel transport it to get a basis
. Parallel transport it to get a basis 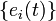 all along
all along  .
This gives an orthonormal basis with
.
This gives an orthonormal basis with 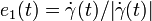 . The Jacobi field can be written in co-ordinates in terms of this basis as
. The Jacobi field can be written in co-ordinates in terms of this basis as 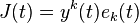 and thus
and thus
and the Jacobi equation can be rewritten as a system
for each  . This way we get a linear ordinary differential equation (ODE).
Since this ODE has smooth coefficients we have that solutions exist for all
. This way we get a linear ordinary differential equation (ODE).
Since this ODE has smooth coefficients we have that solutions exist for all  and are unique, given
and are unique, given 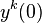 and
and  , for all
, for all  .
.
Examples
Consider a geodesic  with parallel orthonormal frame
with parallel orthonormal frame  ,
, 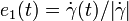 , constructed as above.
, constructed as above.
- The vector fields along
 given by
given by 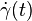 and
and 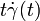 are Jacobi fields.
are Jacobi fields. - In Euclidean space (as well as for spaces of constant zero sectional curvature) Jacobi fields are simply those fields linear in
 .
. - For Riemannian manifolds of constant negative sectional curvature
 , any Jacobi field is a linear combination of
, any Jacobi field is a linear combination of 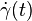 ,
, 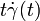 and
and  , where
, where  .
. - For Riemannian manifolds of constant positive sectional curvature
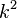 , any Jacobi field is a linear combination of
, any Jacobi field is a linear combination of 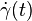 ,
, 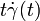 ,
, 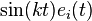 and
and 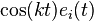 , where
, where  .
. - The restriction of a Killing vector field to a geodesic is a Jacobi field in any Riemannian manifold.
- The Jacobi fields correspond to the geodesics on the tangent bundle (with respect to the metric on
 induced by the metric on
induced by the metric on 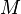 ).
).
See also
- Conjugate points
- Geodesic deviation equation
- Rauch comparison theorem
- N-Jacobi field
References
- [do Carmo] M. P. do Carmo, Riemannian Geometry, Universitext, 1992.