Implicit function
| Part of a series of articles about | ||||||
| Calculus | ||||||
|---|---|---|---|---|---|---|
|
||||||
|
Specialized |
||||||
In mathematics, an implicit equation is a relation of the form , where is a function of several variables (often a polynomial). For example, the implicit equation of the unit circle is .
An implicit function is a function that is defined implicitly by an implicit equation, by associating one of the variables (the value) with the others (the arguments).[1]:204–206 Thus, an implicit function for in the context of the unit circle is defined implicitly by . This implicit equation defines as a function of only if and one considers only non-negative (or non-positive) values for the values of the function.
The implicit function theorem provides conditions under which a relation defines an implicit function.
Examples
Inverse functions
A common type of implicit function is an inverse function. If f is a function of x, then the inverse function of f, called f −1, is the function giving a solution of the equation
for x in terms of y. This solution is
Intuitively, an inverse function is obtained from f by interchanging the roles of the dependent and independent variables. Stated another way, the inverse function gives the solution for x of the equation
Example
The product log is an implicit function giving the solution for x of the equation y − x ex = 0.
Algebraic functions
An algebraic function is a function that satisfies a polynomial equation whose coefficients are themselves polynomials. For example, an algebraic function in one variable x gives a solution for y of an equation
where the coefficients ai(x) are polynomial functions of x. Algebraic functions play an important role in mathematical analysis and algebraic geometry. A simple example of an algebraic function is given by the left side of the unit circle equation:
Solving for y gives an explicit solution:
But even without specifying this explicit solution, it is possible to refer to the implicit solution of the unit circle equation.
While explicit solutions can be found for equations that are quadratic, cubic, and quartic in y, the same is not in general true for quintic and higher degree equations, such as
Nevertheless, one can still refer to the implicit solution y = g(x) involving the multi-valued implicit function g.
Caveats
Not every equation R(x, y) = 0 implies a graph of a single-valued function, the circle equation being one prominent example. Another example is an implicit function given by x − C(y) = 0 where C is a cubic polynomial having a "hump" in its graph. Thus, for an implicit function to be a true (single-valued) function it might be necessary to use just part of the graph. An implicit function can sometimes be successfully defined as a true function only after "zooming in" on some part of the x-axis and "cutting away" some unwanted function branches. Then an equation expressing y as an implicit function of the other variable(s) can be written.
The defining equation R(x, y) = 0 can also have other pathologies. For example, the equation x = 0 does not imply a function f(x) giving solutions for y at all; it is a vertical line. In order to avoid a problem like this, various constraints are frequently imposed on the allowable sorts of equations or on the domain. The implicit function theorem provides a uniform way of handling these sorts of pathologies.
Implicit differentiation
In calculus, a method called implicit differentiation makes use of the chain rule to differentiate implicitly defined functions.
For differentiating an implicit function y(x), defined by an equation R(x, y) = 0, it is not generally possible to solve it explicitly for y and then differentiate. Instead, one can differentiate R(x, y) with respect to x and y and then solve a linear equation in dy / dx for getting explicitly the derivative in terms of x and y. Even when it is possible to solve explicitly the equation, the resulting formula is, in general, much simpler and easier to use.
Examples
1. Consider for example
This equation is easy to solve for y, giving
where the right side is the explicit form of the function y(x). Differentiation then gives dy/dx = −1. Alternatively, one can totally differentiate the original equation:
Solving for dy/dx gives:
the same answer as obtained previously.
2. An example of an implicit function, for which implicit differentiation is easier than using explicit differentiation, the function y(x) defined by the equation
For differentiating this explicitly with respect to x, one has first to get
and then differentiate this function. This creates two derivatives: one for y > 0 and another for y < 0.
It is substantially easier to implicitly differentiate the original equation:
giving
3. Often, it is impossible to solve explicitly for y, and implicit differentiation is the only possible method of differentiation. An example is the equation
It is impossible to express y explicitly as a function of x and therefore dy/dx cannot be found by explicit differentiation. Using the implicit method, dy/dx can be obtained by differentiating the equation to obtain
where dx/dx = 1. Factoring out dy/dx shows that
which yields the result
which is defined for and .
General formula for derivative of implicit function
If the derivative of the implicit function y(x) is given by[2]:§ 11.5
where Rx and Ry indicate the derivatives of R with respect to x and y.
The above formula comes from using the generalized chain rule to obtain the total derivative—with respect to x—of both sides of R(x, y) = 0:
and hence
Implicit function theorem
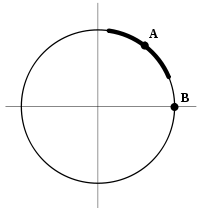
It can be shown that if R(x, y) is given by a smooth submanifold M in R2, and (a, b) is a point of this submanifold such that the tangent space there is not vertical (that is, ∂R/∂y ≠ 0), then M in some small enough neighbourhood of (a, b) is given by a parametrization (x, f(x)) where f is a smooth function.
In less technical language, implicit functions exist and can be differentiated, unless the tangent to the supposed graph would be vertical. In the standard case where we are given an equation
the condition on R can be checked by means of partial derivatives.[2]:§ 11.5
In algebraic geometry
Consider a relation of the form R(x1,..., xn) = 0, where R is a multivariable polynomial. The set of the values of the variables that satisfy this relation is called an implicit curve if n = 2 and an implicit surface if n=3. The implicit equations are the basis of algebraic geometry, whose basic subjects of study are the simultaneous solutions of several implicit equations whose left-hand sides are polynomials. These sets of simultaneous solutions are called affine algebraic sets.
In differential equations
The solutions of differential equations generally appear expressed by an implicit function.[3]
Applications in economics
Marginal rate of substitution
In economics, when the level set R(x, y) = 0 is an indifference curve for the quantities x and y consumed of two goods, the absolute value of the implicit derivative dy/dx is interpreted as the marginal rate of substitution of the two goods: how much more of y one must receive in order to be indifferent to a loss of one unit of x.
Marginal rate of technical substitution
Similarly, sometimes the level set R(L, K) is an isoquant showing various combinations of utilized quantities L of labor and K of physical capital each of which would result in the production of the same given quantity of output of some good. In this case the absolute value of the implicit derivative dK/dL is interpreted as the marginal rate of technical substitution between the two factors of production: how much more capital the firm must use to produce the same amount of output with one less unit of labor.
Optimization
Often in economic theory, some function such as a utility function or a profit function is to be maximized with respect to a choice vector x even though the objective function has not been restricted to any specific functional form. The implicit function theorem guarantees that the first-order conditions of the optimization define an implicit function for each element of the optimal vector x* of the choice vector x. When profit is being maximized, typically the resulting implicit functions are the labor demand function and the supply functions of various goods. When utility is being maximized, typically the resulting implicit functions are the labor supply function and the demand functions for various goods.
Moreover, the influence of the problem's parameters on x*—the partial derivatives of the implicit function—can be expressed as total derivatives of the system of first-order conditions found using total differentiation.
See also
- Functional equation
- Level set
- Marginal rate of substitution
- Implicit function theorem
- Logarithmic differentiation
- Polygonizer
References
- Rudin, Walter (1976). Principles of Mathematical Analysis. McGraw-Hill. ISBN 0-07-054235-X.
- Spivak, Michael (1965). Calculus on Manifolds. HarperCollins. ISBN 0-8053-9021-9.
- Warner, Frank (1983). Foundations of Differentiable Manifolds and Lie Groups. Springer. ISBN 0-387-90894-3.