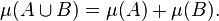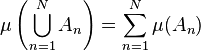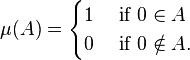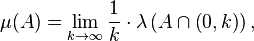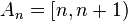Sigma additivity
In mathematics, additivity and sigma additivity (also called countable additivity) of a function defined on subsets of a given set are abstractions of the intuitive properties of size (length, area, volume) of a set.
Additive (or finitely additive) set functions
Let 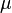 be a function defined on an algebra of sets
be a function defined on an algebra of sets 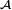 with values in [−∞, +∞] (see the extended real number line). The function
with values in [−∞, +∞] (see the extended real number line). The function 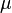 is called additive, or finitely additive, if, whenever A and B are disjoint sets in
is called additive, or finitely additive, if, whenever A and B are disjoint sets in 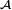 , one has
, one has
(A consequence of this is that an additive function cannot take both −∞ and +∞ as values, for the expression ∞ − ∞ is undefined.)
One can prove by mathematical induction that an additive function satisfies
for any 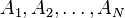 disjoint sets in
disjoint sets in 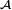 .
.
σ-additive set functions
Suppose that 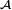 is a σ-algebra. If for any sequence
is a σ-algebra. If for any sequence 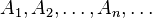 of pairwise disjoint sets in
of pairwise disjoint sets in 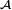 , one has
, one has
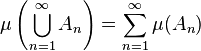 ,
,
we say that μ is countably additive or σ-additive.
Any σ-additive function is additive but not vice versa, as shown below.
τ-additive set functions
Suppose that in addition to a sigma algebra 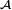 , we have a topology τ. If for any directed family of measurable open sets
, we have a topology τ. If for any directed family of measurable open sets 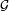 ⊆
⊆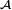 ∩τ,
∩τ,
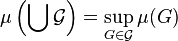 ,
,
we say that μ is τ-additive. In particular, if μ is inner regular then it is τ-additive.[1]
Properties
Basic properties
Useful properties of an additive function μ include the following:
- Either μ(∅) = 0, or μ assigns ∞ to all sets in its domain, or μ assigns −∞ to all sets in its domain.
- If μ is non-negative and A ⊆ B, then μ(A) ≤ μ(B).
- If A ⊆ B and μ(B) − μ(A) is defined, then μ(B \ A) = μ(B) − μ(A).
- Given A and B, μ(A ∪ B) + μ(A ∩ B) = μ(A) + μ(B).
Examples
An example of a σ-additive function is the function μ defined over the power set of the real numbers, such that
If 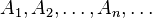 is a sequence of disjoint sets of real numbers, then either none of the sets contains 0, or precisely one of them does. In either case, the equality
is a sequence of disjoint sets of real numbers, then either none of the sets contains 0, or precisely one of them does. In either case, the equality
holds.
See measure and signed measure for more examples of σ-additive functions.
An additive function which is not σ-additive
An example of an additive function which is not σ-additive is obtained by considering μ, defined over the Lebesgue sets of the real numbers by the formula
where λ denotes the Lebesgue measure and lim the Banach limit.
One can check that this function is additive by using the linearity of the limit. That this function is not σ-additive follows by considering the sequence of disjoint sets
for n=0, 1, 2, ... The union of these sets is the positive reals, and μ applied to the union is then one, while μ applied to any of the individual sets is zero, so the sum of μ(An) is also zero, which proves the counterexample.
Generalizations
One may define additive functions with values in any additive monoid (for example any group or more commonly a vector space). For sigma-additivity, one needs in addition that the concept of limit of a sequence be defined on that set. For example, spectral measures are sigma-additive functions with values in a Banach algebra. Another example, also from quantum mechanics, is the positive operator-valued measure.
See also
- signed measure
- measure (mathematics)
- additive map
- subadditive function
- σ-finite measure
- Hahn–Kolmogorov theorem
This article incorporates material from additive on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
References
- ↑ D.H. Fremlin Measure Theory, Volume 4, Torres Fremlin, 2003.