Continuum (topology)
In the mathematical field of point-set topology, a continuum (plural: "continua") is a nonempty compact connected metric space, or, less frequently, a compact connected Hausdorff space. Continuum theory is the branch of topology devoted to the study of continua.
Definitions
- A continuum that contains more than one point is called nondegenerate.
- A subset A of a continuum X such that A itself a continuum is called a subcontinuum of X. A space homeomorphic to a subcontinuum of the Euclidean plane R2 is called a planar continuum.
- A continuum X is homogeneous if for every two points x and y in X, there exists a homeomorphism h: X → X such that h(x) = y.
- A Peano continuum is a continuum that is locally connected at each point.
- An indecomposable continuum is a continuum that cannot be represented as the union of two proper subcontinua. A continuum X is hereditarily indecomposable if every subcontinuum of X is indecomposable.
- The dimension of a continuum usually means its topological dimension. A one-dimensional continuum is often called a curve.
Examples
- An arc is a space homeomorphic to the closed interval [0,1]. If h: [0,1] → X is a homeomorphism and h(0) = p and h(1) = q then p and q are called the endpoints of X; one also says that X is an arc from p to q. An arc is the simplest and most familiar type of a continuum. It is one-dimensional, arcwise connected, and locally connected.
- Topologist's sine curve is a subset of the plane that is the union of the graph of the function f(x) = sin(1/x), 0 < x ≤ 1 with the segment −1 ≤ y ≤ 1 of the y-axis. It is a one-dimensional continuum that is not arcwise connected, and it is locally disconnected at the points along the y-axis.
- The Warsaw circle is obtained by "closing up" the topologist's sine curve by an arc connecting (0,−1) and (1,sin(1)). It is a one-dimensional continuum whose homotopy groups are all trivial, but it is not a contractible space.
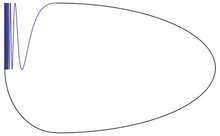
Warsaw circle
- An n-cell is a space homeomorphic to the closed ball in the Euclidean space Rn. It is contractible and is the simplest example of an n-dimensional continuum.
- An n-sphere is a space homeomorphic to the standard n-sphere in the (n + 1)-dimensional Euclidean space. It is an n-dimensional homogeneous continuum that is not contractible, and therefore different from an n-cell.
- The Hilbert cube is an infinite-dimensional continuum.
- Solenoids are among the simplest examples of indecomposable homogeneous continua. They are neither arcwise connected nor locally connected.
- Sierpinski carpet, also known as the Sierpinski universal curve, is a one-dimensional planar Peano continuum that contains a homeomorphic image of any one-dimensional planar continuum.
- Pseudo-arc is a homogeneous hereditarily indecomposable planar continuum.
Properties
There are two fundamental techniques for constructing continua, by means of nested intersections and inverse limits.
- If {Xn} is a nested family of continua, i.e. Xn ⊇ Xn+1, then their intersection is a continuum.
- If {(Xn, fn)} is an inverse sequence of continua Xn, called the coordinate spaces, together with continuous maps fn: Xn+1 → Xn, called the bonding maps, then its inverse limit is a continuum.
A finite or countable product of continua is a continuum.
See also
References
Sources
- Sam B. Nadler, Jr, Continuum theory. An introduction. Pure and Applied Mathematics, Marcel Dekker. ISBN 0-8247-8659-9.
External links
- Open problems in continuum theory
- Examples in continuum theory
- Continuum Theory and Topological Dynamics, M. Barge and J. Kennedy, in Open Problems in Topology, J. van Mill and G.M. Reed (Editors) Elsevier Science Publishers B.V. (North-Holland), 1990.
- Hyperspacewiki
| ||||||||||||||||
This article is issued from Wikipedia - version of the 4/1/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.