Centered nonagonal number

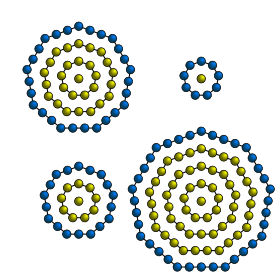
A centered nonagonal number is a centered figurate number that represents a nonagon with a dot in the center and all other dots surrounding the center dot in successive nonagonal layers. The centered nonagonal number for n is given by the formula[1]

Multiplying the (n - 1)th triangular number by 9 and then adding 1 yields the nth centered nonagonal number, but centered nonagonal numbers have an even simpler relation to triangular numbers: every third triangular number (the 1st, 4th, 7th, etc.) is also a centered nonagonal number.[1]

Thus, the first few centered nonagonal numbers are[1]

1, 10, 28, 55, 91, 136, 190, 253, 325, 406, 496, 595, 703, 820, 946.

The list above includes the perfect numbers 28 and 496. All even perfect numbers are triangular numbers whose index is an odd Mersenne prime.[2] Since every Mersenne prime greater than 3 is congruent to 1 modulo 3, it follows that every even perfect number greater than 6 is a centered nonagonal number.

In 1850, Sir Frederick Pollock conjectured that every natural number is the sum of at most eleven centered nonagonal numbers, which has been neither proven nor disproven.[3]

See also

References

  1. 1 2 3 "Sloane's A060544". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  2. ↑ Koshy, Thomas (2014), Pell and Pell–Lucas Numbers with Applications, Springer ISBN 1461484898, 9781461484899, p. 90.
  3. ↑ Dickson, L. E. (2005), Diophantine Analysis, History of the Theory of Numbers, 2, New York: Dover, pp. 22–23.
This article is issued from Wikipedia - version of the 10/29/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.