Apollonius of Perga
Apollonius of Perga (Greek: Ἀπολλώνιος; Latin: Apollonius Pergaeus; c. 262 – c. 190 BC) was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Johannes Kepler, Isaac Newton, and René Descartes. Apollonius gave the ellipse, the parabola, and the hyperbola their modern names. The hypothesis of eccentric orbits, or equivalently, deferent and epicycles, to explain the apparent motion of the planets and the varying speed of the Moon, is also attributed to him. Ptolemy describes Apollonius' theorem in the Almagest XII.1. Apollonius also researched the lunar history, for which he is said to have been called Epsilon (ε). The crater Apollonius on the Moon is named in his honor. He is one of the ancient geometers.
Conics
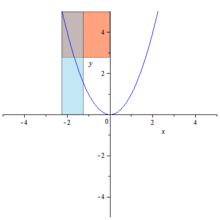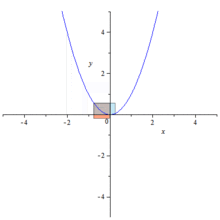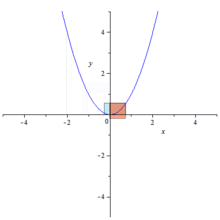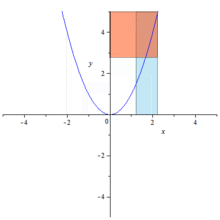
The degree of originality of the Conics (Κωνικά) can best be judged from Apollonius's own prefaces. Books i–iv he describes as an "elementary introduction" containing essential principles, while the other books are specialized investigations in particular directions. He then claims that, in Books i–iv, he only works out the generation of the curves and their fundamental properties presented in Book i more fully and generally than did earlier treatises, and that a number of theorems in Book iii and the greater part of Book iv are new. Allusions to predecessor's works, such as Euclid's four Books on Conics, show a debt not only to Euclid but also to Conon and Nicoteles.
He defines the fundamental conic property as the equivalent of the Cartesian equation applied to oblique axes—i.e., axes consisting of a diameter and the tangent at its extremity—that are obtained by cutting an oblique circular cone. The way the cone is cut does not matter. He shows that the oblique axes are only a particular case after demonstrating that the basic conic property can be expressed in the same form with reference to any new diameter and the tangent at its extremity. It is the form of the fundamental property (expressed in terms of the "application of areas") that leads him to give these curves their names: parabola, ellipse, and hyperbola. Thus Books v–vii are clearly original.
In Book v, Apollonius treats normals as minimum and maximum straight lines drawn from given points to the curve (independently of tangent properties); discusses how many normals can be drawn from particular points; finds their feet by construction; and gives propositions that both determine the center of curvature at any point and lead at once to the Cartesian equation of the evolute of any conic.

Apollonius in the Conics further developed a method that is so similar to analytic geometry that his work is sometimes thought to have anticipated the work of Descartes by some 1800 years. His application of reference lines, a diameter and a tangent, is essentially no different than our modern use of a coordinate frame, where the distances measured along the diameter from the point of tangency are the abscissas, and the segments parallel to the tangent and intercepted between the axis and the curve are the ordinates. He further developed relations between the abscissas and the corresponding ordinates that are equivalent to rhetorical equations of curves. However, although Apollonius came close to developing analytic geometry, he did not manage to do so since he did not take into account negative magnitudes and in every case the coordinate system was superimposed upon a given curve a posteriori instead of a priori. That is, equations were determined by curves, but curves were not determined by equations. Coordinates, variables, and equations were subsidiary notions applied to a specific geometric situation.[1]
Other works
Pappus mentions other treatises of Apollonius:
- Λόγου ἀποτομή, De Rationis Sectione ("Cutting of a Ratio")
- Χωρίου ἀποτομή, De Spatii Sectione ("Cutting of an Area")
- Διωρισμένη τομή, De Sectione Determinata ("Determinate Section")
- Ἐπαφαί, De Tactionibus ("Tangencies")[2]
- Νεύσεις, De Inclinationibus ("Inclinations")
- Τόποι ἐπίπεδοι, De Locis Planis ("Plane Loci").
Each of these was divided into two books, and—with the Data, the Porisms, and Surface-Loci of Euclid and the Conics of Apollonius—were, according to Pappus, included in the body of the ancient analysis.
De Rationis Sectione
De Rationis Sectione sought to resolve a simple problem: Given two straight lines and a point in each, draw through a third given point a straight line cutting the two fixed lines such that the parts intercepted between the given points in them and the points of intersection with this third line may have a given ratio.
De Spatii Sectione
De Spatii Sectione discussed a similar problem requiring the rectangle contained by the two intercepts to be equal to a given rectangle.
In the late 17th century, Edward Bernard discovered a version of De Rationis Sectione in the Bodleian Library. Although he began a translation, it was Halley who finished it and included it in a 1706 volume with his restoration of De Spatii Sectione.
De Sectione Determinata
De Sectione Determinata deals with problems in a manner that may be called an analytic geometry of one dimension; with the question of finding points on a line that were in a ratio to the others.[3] The specific problems are: Given two, three or four points on a straight line, find another point on it such that its distances from the given points satisfy the condition that the square on one or the rectangle contained by two has a given ratio either (1) to the square on the remaining one or the rectangle contained by the remaining two or (2) to the rectangle contained by the remaining one and another given straight line. Several have tried to restore the text to discover Apollonius's solution, among them Snellius (Willebrord Snell, Leiden, 1698); Alexander Anderson of Aberdeen, in the supplement to his Apollonius Redivivus (Paris, 1612); and Robert Simson in his Opera quaedam reliqua (Glasgow, 1776), by far the best attempt.[4]
De Tactionibus
- For more information, see Problem of Apollonius.
De Tactionibus embraced the following general problem: Given three things (points, straight lines, or circles) in position, describe a circle passing through the given points and touching the given straight lines or circles. The most difficult and historically interesting case arises when the three given things are circles. In the 16th century, Vieta presented this problem (sometimes known as the Apollonian Problem) to Adrianus Romanus, who solved it with a hyperbola. Vieta thereupon proposed a simpler solution, eventually leading him to restore the whole of Apollonius's treatise in the small work Apollonius Gallus (Paris, 1600). The history of the problem is explored in fascinating detail in the preface to J. W. Camerer's brief Apollonii Pergaei quae supersunt, ac maxime Lemmata Pappi in hos Libras, cum Observationibus, &c (Gothae, 1795, 8vo).
De Inclinationibus
The object of De Inclinationibus was to demonstrate how a straight line of a given length, tending towards a given point, could be inserted between two given (straight or circular) lines. Though Marin Getaldić and Hugo d'Omerique (Geometrical Analysis, Cadiz, 1698) attempted restorations, the best is by Samuel Horsley (1770).[4]
De Locis Planis
De Locis Planis is a collection of propositions relating to loci that are either straight lines or circles. Since Pappus gives somewhat full particulars of its propositions, this text has also seen efforts to restore it, not only by P. Fermat (Oeuvres, i., 1891, pp. 3–51) and F. Schooten (Leiden, 1656) but also, most successfully of all, by R. Simson (Glasgow, 1749).[4]
Additional works
Ancient writers refer to other works of Apollonius that are no longer extant:
- Περὶ τοῦ πυρίου, On the Burning-Glass, a treatise probably exploring the focal properties of the parabola
- Περὶ τοῦ κοχλίου, On the Cylindrical Helix (mentioned by Proclus)
- A comparison of the dodecahedron and the icosahedron inscribed in the same sphere
- Ἡ καθόλου πραγματεία, a work on the general principles of mathematics that perhaps included Apollonius's criticisms and suggestions for the improvement of Euclid's Elements
- Ὠκυτόκιον ("Quick Bringing-to-birth"), in which, according to Eutocius, Apollonius demonstrated how to find closer limits for the value of π (pi) than those of Archimedes, who calculated 3+1/7 as the upper limit (3.1428571, with the digits after the decimal point repeating) and 3+10/71 as the lower limit (3.1408456338028160, with the digits after the decimal point repeating)
- an arithmetical work (see Pappus) on a system both for expressing large numbers in language more everyday than that of Archimedes' The Sand Reckoner and for multiplying these large numbers
- a great extension of the theory of irrationals expounded in Euclid, Book x., from binomial to multinomial and from ordered to unordered irrationals (see extracts from Pappus' comm. on Eucl. x., preserved in Arabic and published by Woepke, 1856).
Published editions
The best editions of the works of Apollonius are the following:
- Apollonii Pergaei Conicorum libri quatuor, ex versione Frederici Commandini (Bononiae, 1566), fol.
- Apollonii Pergaei Conicorum libri octo, et Sereni Antissensis de Sectione Cylindri et Coni libri duo (Oxoniae, 1710), fol. (this is the monumental edition of Edmund Halley)
- the edition of the first four books of the Conics given in 1675 by Isaac Barrow
- Apollonii Pergaei de Sectione, Rationis libri duo: Accedunt ejusdem de Sectione Spatii libri duo Restituti: Praemittitur, &c., Opera et Studio Edmundi Halley (Oxoniae, 1706), 4to
- a German translation of the Conics by Paul Heinrich Balsam (Berlin, 1861)
- The definitive Greek text is the edition of Heiberg (Apollonii Pergaei quae Graece exstant Opera, Leipzig, 1891–1893)
- T. L. Heath, Apollonius, Treatise on Conic Sections (Cambridge, 1896)
- The Arabic translation of the Books V–VII was first published in two volumes by Springer Verlag in 1990 (ISBN 0-387-97216-1), volume 9 in the "Sources in the history of mathematics and physical sciences" series. The edition was produced by G. J. Toomer and provided with an English translation and various commentaries.
- Conics: Books I–III translated by R. Catesby Taliaferro, published by Green Lion Press (ISBN 1-888009-05-5). (An English translation of Book IV by Michael N. Fried is also available from the same publisher. ISBN 1-888009-20-9)
- Apollonius de Perge, Coniques: Texte grec et arabe etabli, traduit et commenté (De Gruyter, 2008–2010), eds. R. Rashed, M. Decorps-Foulquier, M. Federspiel. (This is a new edition of the surviving Greek text (Books I–IV), a full edition of the surviving Arabic text (Books I–VII) with French translation and commentaries.)
- Apollonius of Perga's Conica: Text, Context, Subtext. By Michael N. Fried and Sabetai Unguru (Brill).
- Edmund Halley's Reconstruction of the Lost Book of Apollonius' Conics. By Michael N. Fried (ISBN 1461401453).
See also
- Apollonian circles
- Apollonian gasket
- Apollonian network
- Circles of Apollonius
- Descartes' theorem
- Problem of Apollonius
- Apollonius' theorem
Notes
- ↑ Boyer, Carl B. (1991). "Apollonius of Perga". A History of Mathematics (Second ed.). John Wiley & Sons, Inc. pp. 156–157. ISBN 0-471-54397-7.
The method of Apollonius in the Conics in many respects are so similar to the modern approach that his work sometimes is judged to be an analytic geometry anticipating that of Descartes by 1800 years. The application of references lines in general, and of a diameter and a tangent at its extremity in particular, is, of course, not essentially different from the use of a coordinate frame, whether rectangular or, more generally, oblique. Distances measured along the diameter from the point of tangency are the abscissas, and segments parallel to the tangent and intercepted between the axis and the curve are the ordinates. The Apollonian relationship between these abscissas and the corresponding ordinates are nothing more nor less than rhetorical forms of the equations of the curves. However, Greek geometric algebra did not provide for negative magnitudes; moreover, the coordinate system was in every case superimposed a posteriori upon a given curve in order to study its properties. There appear to be no cases in ancient geometry in which a coordinate frame of reference was laid down a priori for purposes of graphical representation of an equation or relationship, whether symbolically or rhetorically expressed. Of Greek geometry we may say that equations are determined by curves, but not that curves are determined by equations. Coordinates, variables, and equations were subsidiary notions derived from a specific geometric situation; [...] That Apollonius, the greatest geometer of antiquity, failed to develop analytic geometry, was probably the result of a poverty of curves rather than of thought. General methods are not necessary when problems concern always one of a limited number of particular cases.
- ↑ Dana Mackenzie. "A Tisket, a Tasket, an Apollonian Gasket". American Scientist. 98, January–February 2010 (1): 10–14.
- ↑ Boyer, Carl B. (1991). "Apollonius of Perga". A History of Mathematics (Second ed.). John Wiley & Sons, Inc. p. 142. ISBN 0-471-54397-7.
The Apollonian treatise On Determinate Section dealt with what might be called an analytic geometry of one dimension. It considered the following general problem, using the typical Greek algebraic analysis in geometric form: Given four points A, B, C, D on a straight line, determine a fifth point P on it such that the rectangle on AP and CP is in a given ratio to the rectangle on BP and DP. Here, too, the problem reduces easily to the solution of a quadratic; and, as in other cases, Apollonius treated the question exhaustively, including the limits of possibility and the number of solutions.
- 1 2 3
 Chisholm, Hugh, ed. (1911). "Apollonius of Perga". Encyclopædia Britannica (11th ed.). Cambridge University Press.
Chisholm, Hugh, ed. (1911). "Apollonius of Perga". Encyclopædia Britannica (11th ed.). Cambridge University Press.
References
- Alhazen (1985). Hogendijk, J.P., ed. Ibn al-Haytham's Completion of the "Conics". New York: Springer Verlag.
- Apollonius. Apollonii Pergaei quae Graece exstant cum commentariis antiquis. Edited by I. L. Heiberg. 2 volumes. (Leipzig: Teubner, 1891/1893).
- Apollonius. Apollonius of Perga Conics Books I–III. Translated by R. Catesby Taliaferro. (Santa Fe: Green Lion Press, 1998).
- Apollonius. Apollonius of Perga Conics Book IV. Translated with introduction and notes by Michael N. Fried. (Santa Fe: Green Lion Press, 2002).
- Fried, Michael N.; Unguru, Sabetai (2001). Apollonius of Perga’s Conica: Text, Context, Subtext. Leiden: Brill.
- Knorr, W. R. (1986). Ancient Tradition of Geometric Problems. Cambridge, MA: Birkhauser Boston.
- Neugebauer, Otto (1975). A History of Ancient Mathematical Astronomy. New York: Springer-Verlag.
- Pappus of Alexandria (1986). Jones, A, ed. Book 7 of the "Collection". New York: Springer-Verlag.
- Toomer, G.J. (1970). "Apollonius of Perga". Dictionary of Scientific Biography. 1. New York: Charles Scribner's Sons. pp. 179–193. ISBN 0-684-10114-9.
- Zeuthen, H. G. (1886). Die Lehre von den Kegelschnitten im Altertum. Copenhagen: Höst and Sohn.
- Attribution
 This article incorporates text from a publication now in the public domain: Heath, T. L. (1911). "Apollonius of Perga". In Chisholm, Hugh. Encyclopædia Britannica (11th ed.). Cambridge University Press.
This article incorporates text from a publication now in the public domain: Heath, T. L. (1911). "Apollonius of Perga". In Chisholm, Hugh. Encyclopædia Britannica (11th ed.). Cambridge University Press.
External links
| Wikimedia Commons has media related to Apollonius of Perga. |
- Conic Sections of Apollonius at Convergence
- O'Connor, John J.; Robertson, Edmund F., "Apollonius of Perga", MacTutor History of Mathematics archive, University of St Andrews.
- The Works of Apollonius of Perga online
- Text in Classical Greek: PDF scans of Heiberg's edition of the Conic Sections of Apollonius of Perga, now in the public domain
- In English translation: Treatise on the Conic Sections, trans. T.L. Heath
- Conicorum libri octo, et Sereni antissensis de sectione dylindri & coni libri duo (1710) - Linda Hall Library