19 equal temperament

In music, 19 equal temperament, called 19-TET, 19-EDO ("Equal Division of the Octave"), or 19-ET, is the tempered scale derived by dividing the octave into 19 equal steps (equal frequency ratios). Each step represents a frequency ratio of 21/19, or 63.16 cents (![]() Play ). Because 19 is a prime number, one can use any interval from this tuning system to cycle through all possible notes; just as one may cycle through 12-edo on the circle of fifths, the number 7 (of semitones in a fifth in 12-edo) being coprime to 12.
Play ). Because 19 is a prime number, one can use any interval from this tuning system to cycle through all possible notes; just as one may cycle through 12-edo on the circle of fifths, the number 7 (of semitones in a fifth in 12-edo) being coprime to 12.
19-edo is the tuning of the syntonic temperament in which the tempered perfect fifth is equal to 694.737 cents, as shown in Figure 1 (look for the label "19-TET"). On an isomorphic keyboard, the fingering of music composed in 19-edo is precisely the same as it is in any other syntonic tuning (such as 12-edo), so long as the notes are spelled properly—that is, with no assumption of enharmonicity.
History
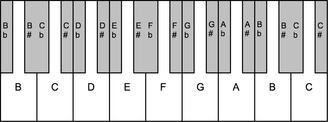


Division of the octave into 19 equal-width steps arose naturally out of Renaissance music theory. The greater diesis, the ratio of four minor thirds to an octave (648:625 or 62.565 cents) was almost exactly a nineteenth of an octave. Interest in such a tuning system goes back to the 16th century, when composer Guillaume Costeley used it in his chanson Seigneur Dieu ta pitié of 1558. Costeley understood and desired the circulating aspect of this tuning. In 1577, music theorist Francisco de Salinas in effect proposed it. Salinas discussed 1/3-comma meantone, in which the fifth is of size 694.786 cents. The fifth of 19-edo is 694.737, which is less than a twentieth of a cent narrower, imperceptible and less than tuning error. Salinas suggested tuning nineteen tones to the octave to this tuning, which fails to close by less than a cent, so that his suggestion is effectively 19-edo. In the 19th century, mathematician and music theorist Wesley Woolhouse proposed it as a more practical alternative to meantone temperaments he regarded as better, such as 50-edo.[3]
The composer Joel Mandelbaum wrote his Ph.D. thesis (1961) on the properties of the 19-edo tuning, and advocated for its use. In his thesis, he argued that it is the only viable system with a number of divisions between 12 and 22, and furthermore that the next smallest number of divisions resulting in a significant improvement in approximating just intervals is the 31 equal temperament.[6] Mandelbaum and Joseph Yasser have written music with 19-edo.[7] Easley Blackwood has stated that 19-edo makes possible "a substantial enrichment of the tonal repertoire".[8]
Scale diagram

The 19-tone system can be represented with the traditional letter names and system of sharps and flats by treating flats and sharps as distinct notes, but identifying B♯ as enharmonic with C♭ and E♯ with F♭. With this interpretation, the 19 notes in the scale become:
| Step (cents) | 63 | 63 | 63 | 63 | 63 | 63 | 63 | 63 | 63 | 63 | 63 | 63 | 63 | 63 | 63 | 63 | 63 | 63 | 63 | |||||||||||||||||||||
| Note name | A | A♯ | B♭ | B | B♯/ C♭ |
C | C♯ | D♭ | D | D♯ | E♭ | E | E♯/ F♭ |
F | F♯ | G♭ | G | G♯ | A♭ | A | ||||||||||||||||||||
| Interval (cents) | 0 | 63 | 126 | 189 | 253 | 316 | 379 | 442 | 505 | 568 | 632 | 695 | 758 | 821 | 884 | 947 | 1011 | 1074 | 1137 | 1200 | ||||||||||||||||||||
The fact that traditional western music maps unambiguously onto this scale makes it easier to perform such music in this tuning than in many other tunings.


Interval size
Here are the sizes of some common intervals and comparison with the ratios arising in the harmonic series; the difference column measures in cents the distance from an exact fit to these ratios. For reference, the difference from the perfect fifth in the widely used 12 equal temperament is 1.955 cents, and the difference from the major third is 13.686 cents.
| Interval Name | Size (steps) | Size (cents) | Midi | Just Ratio | Just (cents) | Midi | Error (cents) |
|---|---|---|---|---|---|---|---|
| Perfect fifth | 11 | 694.74 | 3:2 | 701.96 | −7.22 | ||
| Greater tridecimal tritone | 10 | 631.58 | 13:9 | 636.62 | −5.04 | ||
| Greater septimal tritone, diminished fifth | 10 | 631.58 | 10:7 | 617.49 | +14.09 | ||
| Lesser septimal tritone, augmented fourth | 9 | 568.42 | 7:5 | 582.51 | −14.09 | ||
| Lesser tridecimal tritone | 9 | 568.42 | 18:13 | 563.38 | +5.04 | ||
| Perfect fourth | 8 | 505.26 | 4:3 | 498.04 | +7.22 | ||
| Tridecimal major third | 7 | 442.11 | 13:10 | 454.12 | −10.22 | ||
| Septimal major third | 7 | 442.11 | 9:7 | 435.08 | +7.03 | ||
| Major third | 6 | 378.95 | 5:4 | 386.31 | −7.36 | ||
| Inverted 13th harmonic | 6 | 378.95 | 16:13 | 359.47 | +19.48 | ||
| Minor third | 5 | 315.79 | 6:5 | 315.64 | +0.15 | ||
| Septimal minor third | 4 | 252.63 | 7:6 | 266.87 | −14.24 | ||
| Tridecimal 5/4-tone | 4 | 252.63 | 15:13 | 247.74 | +4.89 | ||
| Septimal whole tone | 4 | 252.63 | 8:7 | 231.17 | +21.46 | ||
| Whole tone, major tone | 3 | 189.47 | 9:8 | 203.91 | −14.44 | ||
| Whole tone, minor tone | 3 | 189.47 | 10:9 | 182.40 | +7.07 | ||
| Greater tridecimal 2/3-tone | 2 | 126.32 | 13:12 | 138.57 | −12.26 | ||
| Lesser tridecimal 2/3-tone | 2 | 126.32 | 14:13 | 128.30 | −1.98 | ||
| Septimal diatonic semitone | 2 | 126.32 | 15:14 | 119.44 | +6.88 | ||
| Diatonic semitone, just | 2 | 126.32 | 16:15 | 111.73 | +14.59 | ||
| Septimal chromatic semitone | 1 | 63.16 | 21:20 | 84.46 | −21.31 | ||
| Chromatic semitone, just | 1 | 63.16 | 25:24 | 70.67 | −7.51 | ||
| Septimal third-tone | 1 | 63.16 | 28:27 | 62.96 | +0.20 |
See also
Sources
- ↑ Milne, A., Sethares, W.A. and Plamondon, J.,"Isomorphic Controllers and Dynamic Tuning: Invariant Fingerings Across a Tuning Continuum", Computer Music Journal, Winter 2007, Vol. 31, No. 4, Pages 15-32.
- ↑ Myles Leigh Skinner (2007). Toward a Quarter-tone Syntax: Analyses of Selected Works by Blackwood, Haba, Ives, and Wyschnegradsky, p.52. ISBN 9780542998478.
- 1 2 Woolhouse, W. S. B. (1835). Essay on Musical Intervals, Harmonics, and the Temperament of the Musical Scale, &c.. J. Souter, London.
- ↑ http://tonalsoft.com/enc/number/19edo.aspx
- ↑ "Diagrams from Yasser's A Theory of Evolving Tonality", MusAnim.com.
- ↑ C. Gamer, Some Combinational Resources of Equal-Tempered Systems. Journal of Music Theory, Vol. 11, No. 1 (Spring, 1967), pp. 32–59
- ↑ Myles Leigh Skinner (2007). Toward a Quarter-tone Syntax: Analyses of Selected Works by Blackwood, Haba, Ives, and Wyschnegradsky, p.51n6. ISBN 9780542998478. Cites Leedy, Douglas (1991). "A Venerable Temperament Rediscovered", Persepctives of New Music 29/2, p.205.
- ↑ Skinner 2007, p.76.
Further reading
- Levy, Kenneth J.,Costeley's Chromatic Chanson, Annales Musicologues: Moyen-Age et Renaissance, Tome III (1955), pp. 213–261.
External links
- M. Joel Mandelbaum, 1961, Multiple Division of the Octave and the Tonal Resources of 19-tone Temperament
- Bucht, Saku and Huovinen, Erkki, Perceived consonance of harmonic intervals in 19-tone equal temperament
- Darreg, Ivor, "A Case For Nineteen", Sonic-Arts.org.
- Howe, Hubert S. Jr., "19-Tone Theory and Applications", Aaron Copland School of Music at Queens College.
- Sethares, William A., "Tunings for 19 Tone Equal Tempered Guitar", Experimental Musical Instruments, Vol. VI, No. 6, April 1991.
- Hair, Bailey, Morrison, Pearson and Parncutt, "Rehearsing Microtonal Music: Grappling with Performance and Intonational Problems" (project summary), Microtonalism.
- ZiaSpace.com - 19tet downloadable mp3s by Elaine Walker of Zia and D.D.T.
- "The Music of Jeff Harrington", Parnasse.com. Jeff Harrington is a composer who has written several pieces for piano in the 19-TET tuning, and there are both scores and MP3's available for download on this site.
- Chris Vaisvil: GR-20 Hexaphonic 19-ET Guitar Improvisation
- Arto Juhani Heino: Artone 19 Guitar Design, naming the 19 note scale Parvatic

